Principles

Introduction

This post defines the fundamental mathematical principles of the Wave Number system. The Wave Number principles introduce the concept of ^{^} Opposite Values (referred to as “Hat” Opposites) and ^v Opposite Values (referred to as “Vee” Opposites). All Opposite Values in the Wave Number system originate from 0, with no positive or negative values. It is important to note that the term “Opposite Value” is used instead of “Opposite Number” because an Opposite Value encompasses more information than a traditional number in classical mathematics.

The symbol for the Wave Number system is . The symbol represents the peaks and troughs of waves and consists of alternating Hats and Vees.

Opposite Values

Each Opposite Value (except zero) consists of three components:

1. Counter: The first is the Counter. This gives the magnitude.  
2. Opposite Type: This component indicates the axis on which the Opposite Value is located. For example, 1^{^} is on the x-axis, 1i^{^} is on the y-axis, and 1j^{^} is on the z-axis. Note that the x-axis does not use a letter designation.
3. Opposite Sign: This component, either ^{^} (called “Hat”) or ^v (called “Vee”), determines which side of 0 on the Wave Number Line the Opposite Value is located.

“Hat” Opposite Values cancel out “Vee” Opposite Values with the same Counter, analogous to how opposite waves cancel each other out. Opposite Values possess a value, whereas Counters do not, as they represent a count or magnitude. While calculations utilize Counters, it is not possible to have a result that is solely a Counter.

The absolute value of an Opposite Value is its magnitude, represented by the Counter. Consequently, Opposite Values with the same Counter but different signs or axes have identical magnitudes.

For example, 1^{^} is the opposite of 1^v, and 1^v is the opposite of 1^{^}. The only difference between 1^v and 1^{^} is their opposition, causing them to cancel each other out when added. Thus, 1^{^} is the additive inverse of 1^v, and vice versa. This principle forms the foundation of Wave Numbers:

1^{^}+ 1^v = 0

The Wave Number system is built upon this equation.

This blog later describes a full set of axioms for Wave Numbers.

The Wave Number system only uses Opposite Values compared to classical mathematics that uses real and imaginary numbers.

Design Principle

In designing the Wave Number system an effort has been made to follow the algebraic permanence principle:

“The principle states that if we want to extend the definition of a basic algebraic operation beyond its original domain (e.g., from the set N of natural numbers to the set Z of integers), then among all logically possible (non-contradictory) extensions the one to be chosen is that which best preserves the rules of calculation.“

Wave Number Lines

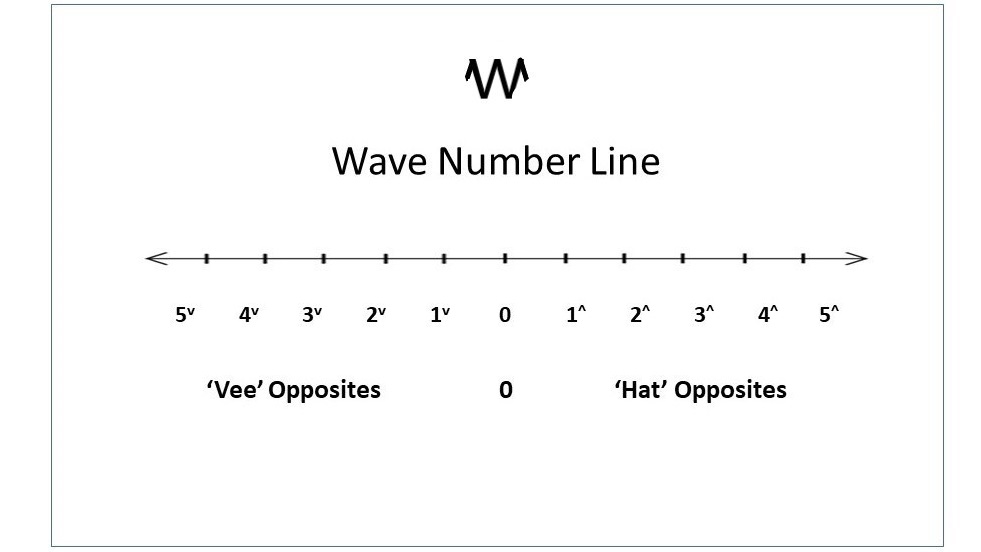
The next component of the Wave Number Principles is the Wave Number lines. Each dimension contributes its own unique Wave Number line.

The notation R followed by the number of dimensions in the space represents the various Wave Number coordinate systems. For example, the Wave Number line for one dimension is denoted as R1, which is equivalent to the classical number line as in the diagram above.

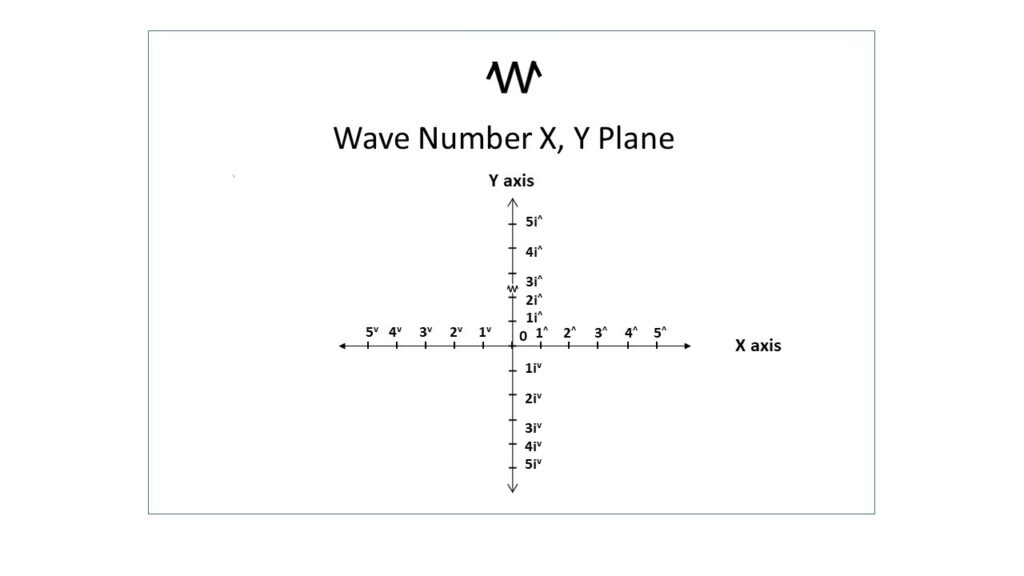
The Wave Number lines for two dimensions, denoted as R2, correspond to the classical x-y plane as in the diagram above. Similarly, the x, y, and z axes are utilized in the Wave Number lines for the three-dimensional system, denoted as R3, analogous to the classical three-dimensional coordinate system.

Opposite Values on the x-axis are in the form 1^{^} and 1^v, on the y-axis in the form 1i^{^} and 1i^v and on the z-axis in the form 1j^{^} and 1j^v.

Typically, the Opposite Values 1i^{^}, 1i^v, 1j^{^}, and  1j^v are written as i^{^}, i^v , j^{^} and j^v , with the Counter 1 implied. These Opposite Values, along with 1^{^} and 1^v , are referred to as unitaries.

According to the algebraic permanence principle, each dimension adheres to the same mathematical rules. Higher dimensions are incorporated using the same rules. Each axis contains 2 unitaries. A unitary Opposite Value has a magnitude of 1. In R1, the unitaries are 1^{^} and 1^v. In R2, they are 1^{^}, 1^v,  i^{^} and i^v, and so on.

Coordinate Systems

The Wave Number system utilizes Cartesian coordinates represented as Opposite Values. This allows for the addition of coordinates and multiplication by scalars. In classical mathematics, Cartesian coordinates cannot be multiplied together without introducing complex numbers.

In the Wave Number system, there is no distinction between a complex number system and a two-dimensional system for real values. All numbers are treated as real, permitting the direct multiplication of Cartesian coordinates.

Zero

In classical mathematics, zero (0) is not considered a number in the traditional sense, but it is extremely useful. The Wave Number system treats zero similarly to classical mathematics, considering it a special Opposite Value. Zero serves as a placeholder indicating the absence of a quantity, aiding in the representation of numbers. It marks the point on an axis where Opposite Values of different Opposite Signs converge, effectively representing the origin and denoting a state of lacking of value or emptiness.

The primary difference in the use of zero in the Wave Number system compared to classical mathematics is that no other Opposite Value is less than or equal to zero. Consequently, the concept of “less than” is redefined based on the magnitudes represented by the Counters of Opposite Values. Thus, all other Opposite Values are considered greater than zero.

Hats and Vees

A Wave Number can have either a ^{^} or a ^v orientation. Visualize a ^{^} Opposite Value as directed upward or to the right in R2, and a ^v Opposite Value as directed downward or to the left. This convention is arbitrary and could be reversed. The key concept is that they are opposites and can cancel each other out.

No Subtraction

A fundamental principle of the Wave Numbers system is the absence of the concept of negativity. Similar to the dichotomy of good and evil, the concept of positivity becomes irrelevant without its negative counterpart. Wave Numbers are represented by ^{^} and ^v Opposite Values that can cancel each other out.

As a result, the subtraction operation is unnecessary. While the addition sign is retained for clarity, it is not essential. It is assumed that all Opposite Values in an equation are added together. Historically, Diophantus did not find it necessary to use an addition sign. In the Wave Numbers system, the addition sign is used solely as a placeholder between Opposite Values. Instead of interpreting numbers as being added together, they can be seen as interacting in the same way waves do when they meet.

However, it is still necessary at times to determine the difference between two Opposite Values. This is achieved by changing the Opposite Sign of one of the Opposite Values and then adding the two Opposite Values together. This process is known as flipping the Opposite Sign.

Counters

Counters can be visualized as existing on a vertical Counter line that starts at 0 and increases as their magnitudes grow larger. A Counter does not possess a positive or negative value; it reflects size, analogous to height, as it indicates the magnitude of an Opposite Value.

Special cases of Counters include constants such as π (pi), e (Euler’s number) and ϕ (the golden ratio). These constants can be combined with Opposite Types and Signs (^{^}, ^v) to form Opposite Values.

Rotation is a Fundamental Operation

Many differences between the Wave Number system and the classical system arise directly from the fundamental equation 1^{^}+ 1^v = 0. Another principle of the Wave Number system is the treatment of rotation as a fundamental operation, on par with addition and multiplication. Rotation, denoted by the symbol ↺ , moves a point in a unique manner similar to how addition and multiplication operate.

Incorporating Opposite Values and rotation into the Wave Number system leads to the treatment of all Opposite Values in all dimensions as Real Opposite Values.

The same rotation rules apply to numbers in any dimension, although this can yield surprising results for operations such as multiplication and division.

R3 Algebra

The mathematical principles of the Wave Numbers system support an algebra in R3. Later, it will be demonstrated that the results of operations on Wave Numbers in R3. correspond to the results of similar operations on vectors in Quaternions.

Conclusion

In summary, the Wave Numbers system corresponds to the classical number system in R1 and R2. It is only when looking at R3 and higher that significant differences emerge. The Wave Number system applies a consistent approach between the different dimensions. The lack of a free axis of rotation causes the differences between R1, R2 and the rest of the dimensions.

Next: Operations

Previous: About