This post covers more advanced math division in R1 such as with expressions, long division and multiplicative inverses.
Division of Expressions using Long Division
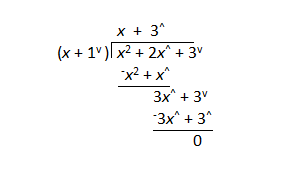
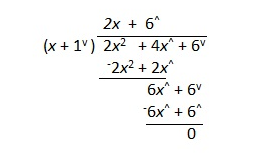
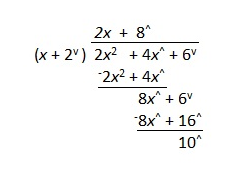
The element of the result above the line is multiplied with the divisor. As the subtraction operation does not exist, the result is flipped and added to the numerator. In the first example:
- The first element of the result is guessed to be x. This is multiplied with the divisor:
- x*(x + 1v) = (x2 + xv)
- The first line under the numerator is calculated as the flip of the result of the previous step:
- –(x2 + xv) = (–x2 + –xv) = (–x2 + x^)
- (x2 + 2x^) and (–x2 + x^) are added to give 3x^
- 3v is brought down from the numerator and the next step proceeds in the same manner.
Note that in the first two examples, the Opposite Value divides evenly. In the last example, there is a remainder of 10^.
Multiplicative Inverses
The theorem for multiplicative inverses shows how the multiplicative inverse is denoted using the flip sign and the Counter 1.
From the theorem, it can be seen that the product of an Opposite Value and its multiplicative inverse is equal to 1^.
a*a-1 = 1^ = a-1*a as a-1 = 1^/a
Examples:
- 1^*1^-1 = 1^(1^/1^)= 1^/1^ = 1^
- Note that x^-1 = xv
- 1v*1v-1 = 1v(1^/1v ) = 1v/1v = 1^
- 3^*3^-1 = 3^(1^/3^) = 3^/3^ = 1^
- 3v*3v-1 = 3v(1^/3v) = 3v/3v = 1^
Other Advanced R1 Division Examples
(a/b)/(c/d) = (ad)/(bc) if b and c are nonzero. For example:
- (6^/2v)/(4^/2^) = 3v/2^ = 3/2v= (6^*2^)/(2v*4^) = 12^/8v = 3/2v
(a/b)/(c/d) = (da)/(cb) if b and c are nonzero. For example:
- (6^/2v)/(4^/2^) = 3v/2^ = 3/2v = (2^*6^)/(4^*2v) = 12^/8v = 3/2v
- (6v/2^)/(4^/2^) = 3v/2^ = 3/2v = (2^*6v)/(4^*2^) = 12v/8^ = 3/2v
(ac)/(bc) = a/b if b and c are nonzero. For example:
- (6^*2v)/(4^*2v) = 12v/8v = 3/2^ = 6^/4^ = 3/2^
- (6v*2^)/(4^*2^) = 12v/8^ = 3/2v = 6v/4^ = 3/2v
a(b/c) = (ab)/c if c is nonzero. For example:
- 6^(4v/2^) = 6^*2v = 12v = (6^*4v)/2^ = 24v/2^ = 12v
- 6v(4v/2^) = 6v*2v = 12^ = (6v*4v)/2^ = 24^/2^ = 12^
Finally, (ab)/b = a if b is nonzero. For example:
- (6^*4v)/4v = 24v/4v = 6^
- (6v*4v)/4v = 24^/4v = 6v
Conclusion
Try these examples of advanced R1 division with our online calculator.
Next: Flipping
Previous: Simple Division

