What is Rotation in R2?
The Wave Number principles describe rotation as a fundamental operation. The rotation axioms support this. An R2 rotation moves a point represented by Opposite Values to a location represented by other Opposite Values by a circular movement around a single point axis represented by Opposite Values. The point of rotation remains fixed during rotation.
Note that rotation around a linear axis in R2 is not possible. To rotate around an axis, the axis needs to be perpendicular to the plane being rotated. in R2, any axis chosen is in the x-y plane and so not perpendicular to the plane.
Syntax
Rotation requires an amount of rotation, a single point axis and a starting point. The syntax of the Rotation operation follows where ? represents the point around which the rotation takes place. The default is (0, 0):
(Amount of rotation) ↺? (Opposite Value)
Examples
Take the expression a ↺ b. Here, b is the Operand and a is the Operator and ↺ is the rotation Operation.
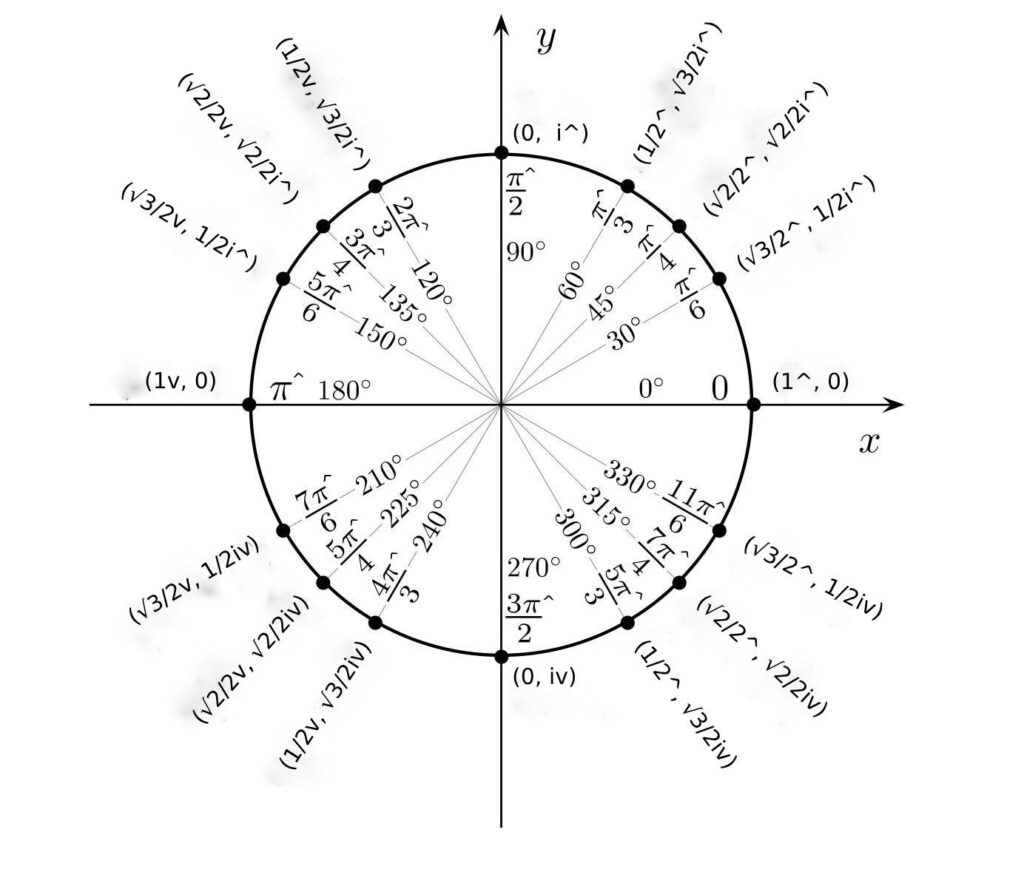
So, π^/2 ↺ 1^ = i^ means take a point located at 1^ on the x-axis and move it to i^ on the y-axis. The rotation is 90^o counterclockwise rotation around the point (0, 0). This is moving the point from (1^, 0) to (0, i^) or to i^ on the y-axis.
In the example, πv/2 ↺ 1^ = iv, the point located at 1^ on the x-axis moves to iv on the y-axis. The rotation is 90vo clockwise around the point (0, 0). This is moving the point from (1^, 0) to (0, iv) or to iv on the y-axis.
Flipping
R2 has two dimensions that use the x and y-axes. Rotation from one side of a number line to the other side of the same number line is possible. This has the effect of switching the Opposite Sign to the other Opposite Sign.
Flipping is the name of this type of R2 rotation. The symbol – represents flipping. For example: –1^ = 1v.
The rotation π^ ↺ 1^ = 1v or πv ↺ 1^ = 1v also represents flipping. In other words, a 180o turn either counterclockwise or clockwise from 1^ moves a point to 1v around the point (0, 0).
Similarly, –i^ = iv. This has the alternative representation of π^ ↺ i^ = iv or πv ↺ i^ = iv. In other words, a 180o turn either counterclockwise or clockwise around (0, 0) from i^ moves a point to iv.
Likewise, –1v = 1^ and –iv = i^.
The Post-It-Note Prop
A physical prop helps to understand two-dimensions. It is best to use something that is small enough to fit between index finger and thumb. A good choice is a post-it note.
Draw the x-axis with the points 3v on the left through 0 in the centre to 3^ on the right. Draw the vertical y-axis with the points 3iv on the bottom through 0 in the centre to 3i^ on the top.
As there are only two-dimensions, treat an imaginary z-axis of rotation as being a dimensionless point at (0, 0) in the centre. This is the one point that remains fixed during rotation.
Rotating the Prop
Holding the post-it note at (0, 0), vertical to the ground, rotate the note 90^o counterclockwise. This brings the point located at (1^, 0) on the x-axis to where i^ had been on the y-axis. A further 90^o rotation brings the point to 1v.
Note that there is a need for an axis point from the next dimension to rotate freely in R1 and R2.
R2 rotation not only allows moving a point on the same axis by flipping, it also allows moving a point to the other axis and to locations between the axes depending on the amount of rotation. This allows a point to be moved to anywhere on a circle in the x-y plane. The radius of the circle for a point (a, b) that is rotated around the origin is given by Pythagoras’ theorem – √(|a|2 + |b|2).
Alternative Points of Rotation
Rotations in R2 differs from R3 in that they must use a point for rotation as opposed to an actual axis. When the point is at (0, 0), the point is an imaginary z-axis. Any other point is an imaginary axis that is parallel to the z-axis. So, rotation around the point (0, 1^) is rotation around an axis through the point (0, 1^) that is parallel to the z-axis. The z-axis is orthogonal to the the x and y axes.
A π^/2 rotation around an imaginary axis at (1^, 0) moves a point at (4^, 0) to (1^, 3i^). It is expressed as π^/2 ↺(1^, 0) (4^, 0) = (1^, 3i^) .
Rotation of a point around itself in R2 leaves the point at the same location. A 122^o counterclockwise turn around an imaginary axis at (1^,iv) leaves the point (1^,iv) at (1^, iv). This is expressed as 122^o ↺(1^,iv) (1^,iv) = (1^,iv).
Conclusion
Try these examples of R2 rotation with our online calculator.
Next: Simple Examples
Previous: Geometry and Trigonometry


One Response
Rotation definition comment 29/11