Operations

Introduction

 

Wave Numbers require a re-evaluation of general mathematical operations such as addition, subtraction, rotation, multiplication and division. Operators, operations, and operands need new definitions within this system.

In Wave Number mathematics, the key distinction between 1^{^} and 1^v is that through interference they cancel each other out when they combine.

Subtraction is not used in Wave Numbers. Calculating the difference between two Opposite Values involves adding them after changing the Opposite Sign of one value using the flip operation (^–). The flip operation, described later, essentially rotates an Opposite Value by π. This is not a subtraction sign but an operation that changes the Opposite Sign (^{^},^v) of an Opposite Value.

Thus, the cancellation effect typically provided by subtraction is achieved in Wave Numbers through addition with the Opposite Sign flipped.

To find the difference involving a variable with an unknown Opposite Sign, precede the variable with a flip sign (^–).

The section on rotation demonstrates that 1^v is equivalent to 1^{^} rotated by an angle of π in either a clockwise or counterclockwise direction. Similarly, 1^{^} is equivalent to 1^v rotated by an angle of π in either direction.

The Wave Number system introduces some new operations. The first is rotication, which multiplies the result of an initial rotation around an axis by the magnitude of the axis of rotation.

Additionally, new operations include rotvision and roticvision. Analogous to how division is the inverse of multiplication, rotvision is the inverse of rotation, and roticvision is the inverse of rotication.

Operators, Operations and Operands

A mathematical operation consists of an Operator, an Operation, and an Operand. For example, consider the expression 1^{^}*1^v  = 1^v. In this context, 1^{^} is the operator, * denotes the operation (multiplication), and 1^v  is the operand. The Opposite Type and Sign of the result depend on the multiplication tables described later.

In Wave Number multiplication, the Operator performs the Operation on the Operand. Specifically, the Operator is the first term in the expression, and the Operand is the second term.

In the context of division, the Operand is the numerator, and the Operator functions as the divisor. While the Operator may be a Counter, the Operand must always be an Opposite Value in both multiplication and division.

For instance, consider the expression 1^/1v  =  1v. Here, 1^ is the Operand, / represents the Operation of division, and 1v serves as the Operator. The sign of the result is determined by the division tables, which will be explained in subsequent sections.

In the context of roots , the Operator specifies the degree of the root, while the Operand represents the Opposite Value for which the root is being calculated.

For rotation, the Operator consists of two components: a radian or degree value that represents an angle of rotation and an axis of rotation. For example, π^{^}indicates a counterclockwise rotation of 180^{o^} around the axis, while π^v represents a clockwise rotation of 180^ov around the axis.  The symbol ↺ denotes the rotation operation. The Operand represents the point being rotated, with an Opposite Value used to describe its position.

Rotication follows the same format as rotation where the symbol for the Operation is R↺.

In the addition operation, add the Operator to the Operand. Both must be Opposite Values.

Addition

In the Wave Number system, only Opposite Values of the same Opposite Type can be consolidated through addition. This process involves adjusting the coordinates of a point on the Wave Number axis according to the types of Opposite Values present.

For example, in R2, the addition of Opposite Values is performed as follows:

(1^{^} + 2i^v) + (2^+ 3iv) = (3^+ 5iv)

Multiplication

In Wave Numbers math multiplication takes into account the ^{^} and ^v signs. When the Operand, which is the first term in a multiplication, is ^{^} then it denotes a 90^^o turn counterclockwise during the operation. If there is a ^v in the first term in the multiplication then it represents a 90^vo turn clockwise. So, i^{^}*1^{^}, in R2, results in the value of i^{^} which is on the y-axis.

Multiplication by a unitary is the equivalent of rotation around the unitary’s axis by 90^^o . In this way unitaries link rotation and multiplication. The section on rotation explains this fully.

Rotation

Introducing the concept of rotation in the Wave Number system gives rise to the notions of R2 and the x-y plane. Consider the expression a ↺ b, where a is the Operator, b is the Operand, and ↺ denotes the rotation Operation.

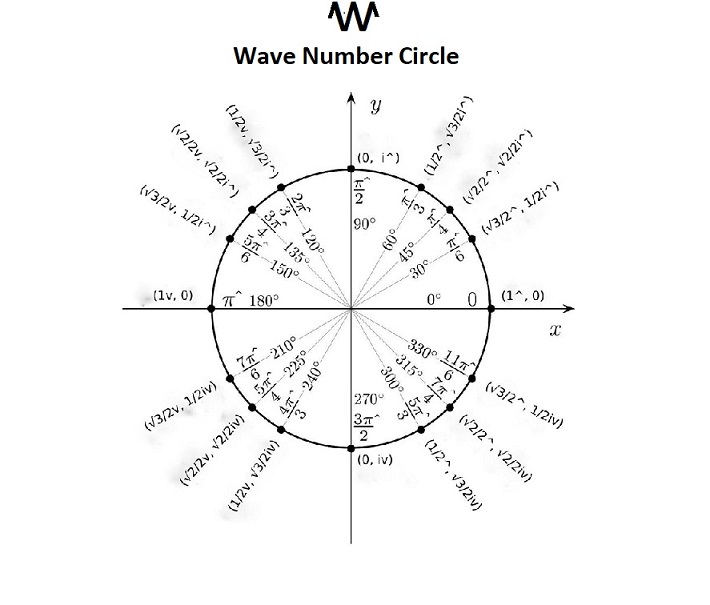
For example, the expression π^{^}/2 ↺ 1^{^} = i^{^} in R2 represents a counterclockwise rotation of 90^^o around an imaginary z-axis. This operation moves the point 1^{^} on the x-axis to i^{^} on the y-axis. Mathematically, this rotation transforms the point from (1^{^}, 0) to (0, i^{^}) , corresponding to i^{^} algebraically.

Similarly, the expression π^v/2 ↺ 1^{^} = i^v represents a clockwise rotation of 90^vo around an imaginary z-axis. The operation moves the point 1^{^}on the x-axis to i^v on the y-axis, transforming the point from (1^{^}, 0) to (0, i^v), which corresponds to i^v algebraically.

Points between the axes are determined as the sum of values on the respective axes. For instance, in R2, the point √2/2^{^} + √2/2i^{^} represents the Cartesian coordinates (√2/2^{^}, √2/2i^{^}). This point results from a 45^^o counterclockwise rotation (or π^{^}/4 radians) of the point (1^{^},0) to (√2/2^{^}, √2/2i^{^}) around the origin (0, 0).

Trigonometric functions such as cosine, sine etc. are Counters as they are ratios, and so magnitudes, and are calculated based on the Counters of a point’s coordinates, as in classical math. When calculating the angle of rotation of points on the x-y plane, the quadrant needs to be taken into account. For example, take the point at (1^{^}, √3^{^}), its radius is . Based on the Counters of its coordinates, its cosine is 1/2 = 0.5 and its sine is √3/2 = 0.866. It’s angle is 60^^o.

Now take the point at , its radius is . Its cosine is and its sine is . It’s angle is .

Note that the ^v coordinates are reflected in the equations by the applying flip signs (^–) to the Counters.

Counters

An operation can involve multiple Counters that interact with each other. For instance, in the expression 6* 4 * 2^, the Counters 6 and 4 are multiplied together.

Counters with flip signs can cancel each other out, as demonstrated by ^–6*^–4*2^ =  6*4*2^. In certain contexts, such as exponentiation and logarithms, Counters may also be added together.

Finally, counters are not standalone and are always used with an Opposite Value.  

Other

The double-dagger symbol is used in certain contexts to denote the Opposite Type and Sign of a variable.

For example, with inverse exponents as in  1 in R3. Here, the double-daggers indicate that the numerator has the same Opposite Type and Sign as . The represents the Opposite Type of , and the superscript denotes the Opposite Sign of .

The symbol ? represents an unknown Opposite Type. The superscript signifies an unknown Opposite Sign. For example 3?^? could represent 3^{^}¸3^v, 3i^{^}, 3i^v, 3j^{^} or 3j^v  in R3.

A preceding ^? indicates an unknown flip sign, which may or may not be present. For example:  ^?mx could be  ^–2x or 2x.

 

Next: Axioms

Previous: Principles