This post provides some simple examples of R2 roots. The calculations behind some of the examples are also shown.
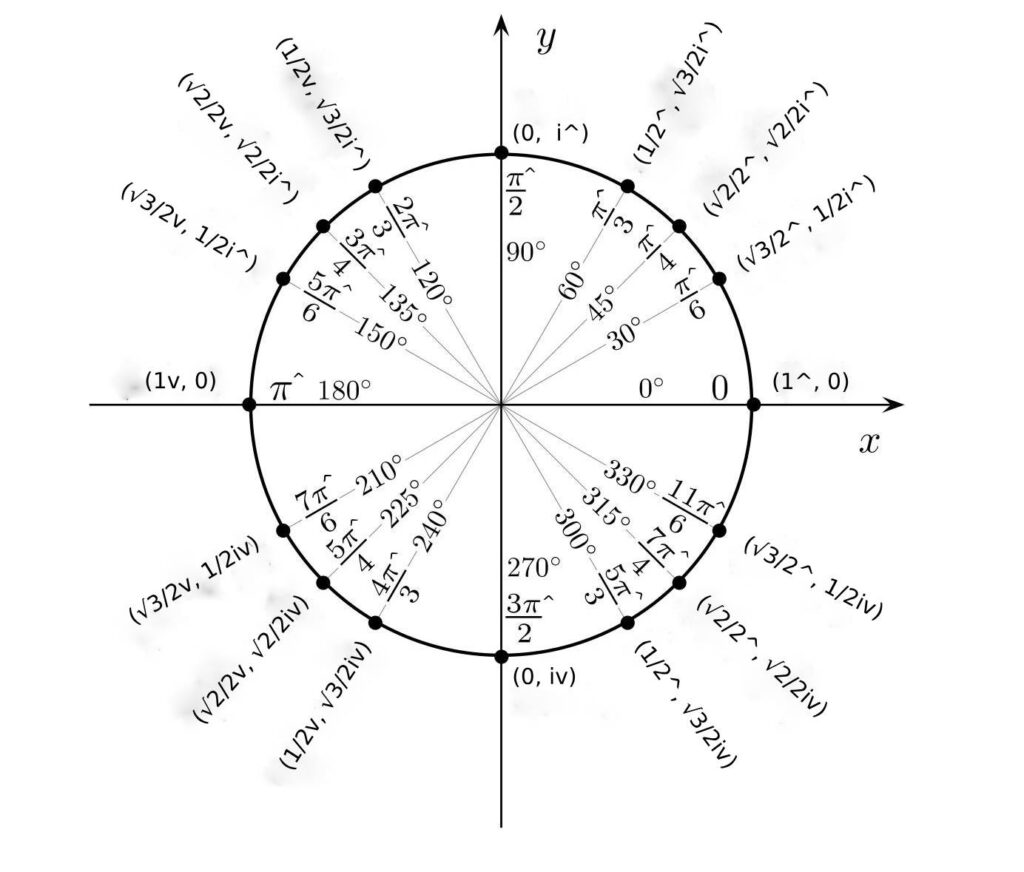
Examples
Firstly, here are some examples of the roots of i^.
- √(i^) = (√2/2^ + √2/2i^) or (√2/2v + √2/2iv)
- 3√(i^) = iv or (√3/2^ + ½i^) etc.
- 4√(i^) = (0.924^ + 0.383i^) etc.
- 5√(i^) = i^ or (0.951^ + 0.309i^) etc.
- 6√(i^) = (0.966^ + 0.259i^) etc.
- 7√(i^) = iv or (0.975^ + 0.223i^)etc.
- 8√(i^) = (0.981^ + 0.195i^) etc.
- 9√(i^) = i^ or (0.985^ + 0.174i^)etc.
- 10√(i^) = (0.988^ + 0.156i^) etc.
Secondly, here are examples of the roots of iv.
- √(iv) = (√2/2^ + √2/2iv) or (√2/2v + √2/2i^)
- 3√(iv) = i^ or (√3/2^ + ½iv) etc.
- 4√(iv) = (0.924^ + 0.383iv) etc.
- 5√(iv) = iv or (0.951^ + 0.309iv) etc.
Finally, here are some examples of non unitary roots.
- √(9^) = 3^or 3v;
- √(9v) = 3i^or 3iv
- √(9i^) = 2.12^+ 2.12i^ or 2.12v + 2.12iv
- √(9iv) = 2.12^+ 2.12iv or 2.12v + 2.12i^
Sample Calculations
These calculations show how these simple R2 roots can be multiplied in order to get the original Opposite Value.
- 3√(1^) = (½v + √3/2i^) or (½v + √3/2iv):
- (½v + √3/2i^)3 = (½v + √3/2i^)(¼^ + √3/4iv + √3/4iv + ¾v)
- = (½v + √3/2i^)(½v + √3/2iv)
- = (¼^ + √3/4i^ + √3/4iv + ¾^)
- = 1^
- (½v + √3/2iv)3 = (½v + √3/2iv )(¼^ + √3/4i^ + √3/4i^ + ¾v)
- = (½v + √3/2iv )(½v + √3/2i^)
- = (¼^ + √3/4iv + √3/4i^ + ¾^)
- = 1^
- 3√(i^) = (√3/2^ + i^/2):
- ((√3/2^) + (½i^))3 = ((√3/2^) + (½i^))(( √3/2^) + (½i^))(( √3/2^) + (½i^))
- = ((√3/2^) + (½i^))(( √3/2^)(√3/2^) + (√3/2^)(½i^) + (½i^)( √3/2^) + (½i^)( ½i^))
- = ((√3/2^) + (½i^))( ¾^ + √¾i^ + √¾i^ + ¼v)
- = ((√3/2^) + (½i^))( ½^ + √3/2i^)
- = (√3/4^ + ¾i^ + ¼i^ + √3/4v)
- = i^
- 4√(i^) = (0.924^ + 0.383i^):
- (0.924^ + 0.383i^)4 = (0.924^*0.924^ + 0.924^*0.383i^ + 0.383i^*0.924^ + 0.383i^* 0.383i^)2
- = (0.854^ + 0.354i^ + 0.354i^ + 0.147v)2
- = (0.707^ +0.708i^)2
- = 0.5^ + 0.5i^ + 0.5i^ + 0.5v
- = i^
- 5√(i^) = (0.951^ + 0.309i^):
- (0.951^+0.309i^)5= (0.951^+0.309i^)*(0.951^*0.951^ + 0.951^*0.309i^ + 0.309i^*0.951^ + 0.309i^*0.309i^)2
- = (0.951^ + 0.309i^)*(0.904^ + 0.294i^ + 0.294i^ + 0.095v)2
- = (0.951^ + 0.309i^)*(0.809^ +0.588i^)2
- = (0.951^ + 0.309i^)*(0.654^ + 0.475i^ + 0.475i^ + 0.345v)
- = (0.951^ + 0.309i^)*(0.309^ + 0. 95i^)
- = (0.294^ + 0.903i^ + 0.095i^ + 0.294v)
- = i^
Conclusion
Try these examples of R2 roots with our online calculator.
Next: Roots of Expressions
Previous: Definition

