Quantum – Gates – Haadamard – H

This post shows how R2 Wave Numbers are used with the Haadamard gate. Note that part 1 of the Bellagio circuit uses Haadamard gates.

H  Gate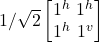 

The Haadmard gate puts |j^{^}> and |j^v> into superposition. It does this by splitting |j^{^}> to |j^{^}> + |j^v> and |j^v> to |j^{^}> + ^–|j^v>. Similarly to other gates, executing the Haadamard gate twice in a row is the equivalent of multiplying by 1^{^} and does not change the state. In effect the first execution moves |j^{^}> and |j^v> into superposition and the second execution returns them to their original state and out of superposition. The gate also works on other states that are already in superposition.

Examples of Haadamard on Basis States

• H |j^{^}> =
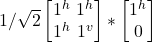
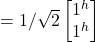  •  = 1/√2|j^{^}> + 1/√2|j^v>

• H ^–|j^{^}> =
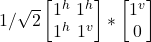
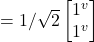  •  = ^–1/√2|j^{^}> + ^–1/√2|j^v>

• H |j^v> =
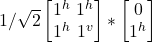
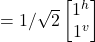  •  = 1/√2|j^{^}> + ^–1/√2|j^v>

• H ^–|j^v> =
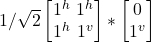
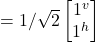  •  = ^–1/√2|j^{^}> + 1/√2|j^v>

Examples of Two Consecutive Haadmard Gates

• 
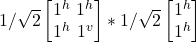
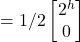  • = |j^{^}>
    • Thus, executing the Haadamard gate on the result of H |j^{^}> above returns the qubit to |j^{^}>

• 
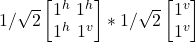
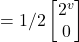  • = ^–|j^{^}>
    • Thus, executing the Haadamard gate on the result of H ^–|j^{^}>above returns the qubit to ^–|j^{^}>

• 
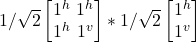
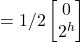  • = |j^v>
    • Thus, executing the Haadamard gate on the result of H |j^v> above returns the qubit to |j^v>

• 
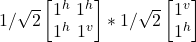
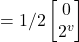  • = ^–|j^v>
    • Thus, executing the Haadamard gate on the result of H ^–|j^v> above returns the qubit to ^–|j^v>

Other Examples

Haadamard Gate in Dirac Notation:

Firstly, H|j^{^}> =

(|j^{^}> <j^{^}|j^{^}> +  |j^{^}><j^v|j^{^}> + |j^v><j^{^}|j^{^}> + ^–| j^v><j^v|j^{^}>)

= ( |j^{^}>*1 + |j^{^}>*0 +|j^v>*1 + ^–|j^v>*0)

 = ( |j^{^}> +|j^v>)

Secondly, H|j^v> =   

(|j^{^}> <j^{^}|j^v> +  |j^{^}><j^v|j^v> + |j^v><j^{^}|j^v> + ^–| j^v><j^v|j^v)

= (|j^{^}>*0 + |j^{^}>*1 +|j^v>*0 + ^–|j^v>*1)

= (|j^{^}> + ^–|j^v >)

Next: Circuits

Previous: Pauli Gates and σf