This post describes is an introduction to quantum circuits in Wave Numbers. It describes the representation of multipart qubits as tensor products. It also shows how multipart qubits are used in multipart addition and Haadamard gates.
Definition
According to Qiskit, ‘A quantum circuit is a computational routine consisting of coherent quantum operations on quantum data, such as qubits. It is an ordered sequence of quantum gates, measurements and resets, which may be conditioned on real-time classical computation. A set of quantum gates is said to be universal if any unitary transformation of the quantum data can be efficiently approximated arbitrarily well as as sequence of gates in the set. Any quantum program can be represented by a sequence of quantum circuits and classical near-time computation.’
The gates discussed in these posts can run on quantum computers. Some other gates are more difficult to run due to error rates.
Multipart Qubit Representation
A circuit can have many qubits. The number of states of a circuit possible is 2n where n = number of qubits. This is because each qubit can be either 0 or 1. Multipart qubits represent qubits in a circuit. It is both possible to describe the multipart qubit in a Dirac state format and in a matrix format. For example: |j^j^> represents a multipart qubit in state format made up of two |j^> qubits. So, using Tensor products, the same multipart qubit can be described using a matrix. For example:
|j^j^> = |j^> ![]() |j^> =
|j^> = 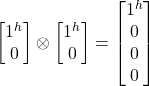
The multipart qubit only represents the product of the qubits. The tensor product represents the relationship between the individual qubits, especially important when entangled. To get the tensor product of a one column matrix with another, multiply the first element of the first column with each of the elements of the second. Each result is stacked in the resulting column. Next, repeat this process for each element of the first column. There are 2 elements in the first column and 4 in the second of the following example. As a result there are 8 elements in the result column.

Two Qubit Multipart Examples
- |j^j^> = |j^>
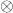 |j^> =
|j^> = 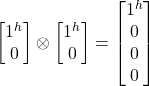
- |j^-j^> = |j^>
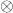 –|j^> = –|j^j^> =
–|j^> = –|j^j^> = 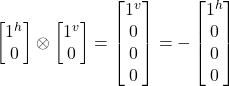
- |j^jv> = |j^>
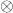 |jv> =
|jv> = 
- |–j^jv> = –|j^>
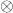 |jv> =
|jv> = 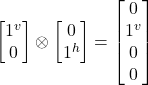
- |–j^-jv> = –|j^>
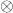 –|jv> =
–|jv> = 
- |jvj^> = |jv>
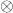 |j^> =
|j^> =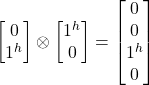
- |–jv-j^> = –|jv>
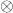 –|j^> =
–|j^> = 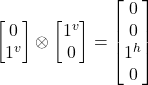
- |jvjv> = |jv>
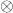 |jv> =
|jv> = 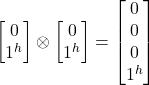
- |–jv-jv>= –|jv>
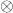 –|jv> =
–|jv> = 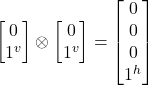
Three Qubit Multipart Examples
- |j^j^j^> = |j^>
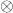 |j^j^> =
|j^j^> = 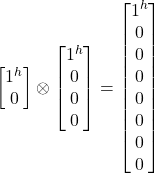
- |j^jvj^> = |j^>
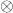 |jvj^> =
|jvj^> = 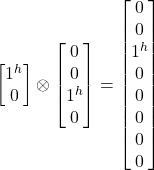
Multipart Addition
Addition is the only mathematical operation available for multipart qubits in a Dirac state format. Should two parts of the multipart qubit have the exact same qubits, they will cancel each other out if one multipart qubit has a flip sign and the other does not. For example: |j^jv> + –|j^jv> = 0.
Even number of flips inside multipart state cancel out. For example: |–j^jv-jv> = |j^jvjv>. Move an odd number of flips outside bracket. For example: |–j^jv-jv-j^> = –|j^jvjvj^>. Note that you cannot flip |j^> to |jv>. This is because these are states that have the matrix representation of ![]() .
.
Two Qubit Multipart Examples
- |j^j^> + |j^j^>= |j^j^> =
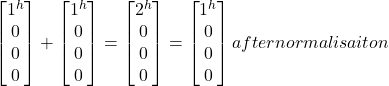 = |j^j^>
= |j^j^>
- |j^j^> + |–j^j^>= |j^j^> + –|j^j^> = 0 =
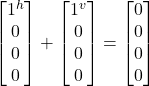 = 0
= 0
- |jvj^> +|j^jv>=
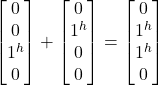 = |jvj^> +|j^jv>
= |jvj^> +|j^jv>
- |j^j^> + –|j^j^>= 0 =
 = 0
= 0
Three Qubit Multipart Examples
- |j^j^j^> + |j^j^j^>= |j^j^j^> =
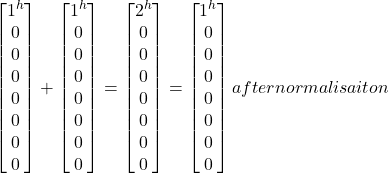 = |j^j^j^>
= |j^j^j^>
- |j^j^j^> + |j^jvj^> =
 = |j^j^j^> + |j^jvj^>
= |j^j^j^> + |j^jvj^>
Multipart Haadamard
The multipart Haadamard gate can split a multipart qubit into two. For example:
- AH2|j^j^> => 1/√2 (|j^j^> + |jvj^>)
- AH2|jvj^> => 1/√2 (|j^j^> + –|jvj^>)
See post on AH2 for details and examples of the multipart Haadamard.
Next: CNOT
Previous: Haadamard Gate

