R3 – Complex Rotations – Comparing Wave Numbers and Quaternion Efficiency

Introduction

This comparison of Wave Numbers and Quaternions evaluates their efficiency based on the rotation operation due to its computational complexity. Computer games and other high quality graphics frequently use rotation operations to implement the physics of movement, making this an important consideration for performance.

Unit of Rotation

The magnitude and unit rotation of a point $(x, y, z)$ are determined by the following calculations:

$R = \sqrt{(|x|^2 + |y|^2 + |z|^2)}$
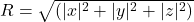
Unit of Rotation $= (x/R, y/R, z/R)$
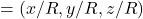
Therefore, the calculation requires 3 multiplications, 1 square root and 3 divisions.

Wave Numbers Processor Workload

The formula for Wave Numbers rotation is:

$v_{rot} = (u_r \cdot v)u_r + sin\theta(u_r \times v) +cos\theta ((u_r \times v)\times u_r)$

Wave Numbers have 3 opposite types, leading to multiplications occurring in sets of 3. This results in the following calculations during rotation:

Unit of Rotation
- 3 multiplications, 1 square root and 3 divisions.
v_rot
- Element 1 – .
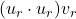  - 3 multiplications and 2 additions to get dot product.
  - 3 multiplications of dot product and $u_r$ .
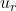- Element 2 – .
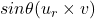  - 6 multiplications and 3 additions to get cross product.
  - 3 multiplications of cross product with sine and 1 sine calculation.
- Element 3 – .
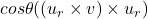  - First cross product already calculated for Element 2.
  - 6 multiplications and 3 additions to get second cross product.
  - 3 multiplications of cross product with cosine and 1 cosine calculation.
- Total: 27 multiplications, 8 additions, 1 square root, 3 divisions, 1 sine and 1 cosine for a single rotation.

Quaternions Processor Workload

Quaternions consist of 4 different types, resulting in multiplications occurring in sets of 4.

Unit of Rotation
- 3 multiplications, 1 square root and 3 divisions.
Quaternion of Rotation.
- The formula for the Quaternion of Rotation is $Qr = cos(\frac{\theta}{2}) + (x_i + y_j + z_k)*sin(\frac{\theta}{2}$ ).
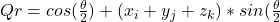- 3 multiplications, 1 division, 1 cosine and 1 sine.
- 16 multiplications of 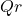$Qr$ and $Qv$ .
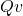- 12 additions to consolidate result into scalar, i, j and k quaternion buckets.
Subtotal per multiplication
- 22 multiplications, 12 additions, 1 square root, 4 divisions, 1 sine and 1 cosine.
Conversion of quaternion to R3
- If there is more than 1 rotation in a chain, then the overall rotation must be calculated starting in reverse. i.e. if the rotation Q1 was followed by Q2 and then Q3 the reverse rotation is (Q3*Q2)*Q1).
  - 16 *(number of rotations – 1) multiplication.
  - 12 * (number of rotations – 1) additions.
  - In the case of 3 rotations this gives 16 * 2 = 32 multiplications and 32 additions.
- 16 multiplications with conjugate of overall reverse rotation followed by 12 additions.
Total
- 38 multiplications, 24 additions, 1 square root, 4 divisions, 1 sine and 1 cosine for a single rotation.

Note: The conversion to R3 in Quaternions only has to take place at the end of a chain of multiplications.

Wave Numbers and Quaternion Efficiency Comparison

1 Multiplication
- Wave Numbers – 27 multiplications, 8 additions, 1 square roots, 3 divisions, 1 sine and 1 cosine.
- Quaternions – 38 multiplications, 24 additions, 1 square roots, 4 divisions, 1 sine and 1 cosine.
2 Multiplications
- Wave Numbers – 54 multiplications, 16 additions, 2 square roots, 6 divisions, 2 sine and 2 cosine.
- Quaternions – 76 multiplications, 48 additions, 2 square roots, 8 divisions, 2 sine and 2 cosine.
3 Multiplications
- Wave Numbers – 81 multiplications, 24 additions, 3 square roots, 9 divisions, 3 sine and 3 cosine.
- Quaternions – 114 multiplications, 72 additions, 3 square roots, 12 divisions, , 3 sine and 3 cosine.
4 Multiplications
- Wave Numbers – 108 multiplications, 32 additions, 4 square roots, 12 divisions, 4 sine and 4 cosine.
- Quaternions – 152 multiplications, 96 additions, 4 square roots, 16 divisions, 4 sine and 4 cosine.

Conclusion

This comparison of Wave Number and Quaternion multiplication demonstrates that Wave Numbers are more efficient. Additionally, Wave Numbers provide a clearer representation as they are always situated in 3D space

Next: Spherical Coordinates

Previous: Example 3

Share to: