Gates
Quantum gates perform operations on qubits and need to relate to the physical process that manipulates qubits. An element of 0 in a gate operating on a 1^ in a qubit is the equivalent of saying stop or that the wave has no probability of getting to that hemisphere.
Dirac’s Notation
Quantum theory is unitary. This is because all quantum states are normalised, i.e. |ψ><ψ| = 1^. For example:
- if |ψ> =
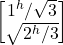
- then |ψ><ψ| = [1^√3 √(2^/3)]
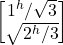
- = 1^√3*1^√3 + √(2^/3)*√(2^/3) = 1^
- then |ψ><ψ| = [1^√3 √(2^/3)]
See Bra-Kets post for more details on Dirac’s notation.
2*2 Quantum Gates
Unitary matrices represent quantum gates. In other words:
- Ut.U = 1^ (U transpose dot U = 1^)
Bra-ket notation allows writing a matrix ,U = ![]() as:
as:
- = U00|j^><j^| + U01|j^><jv| + U10|jv><j^| + U11|jv><jv|
|j^><j^| is a ket-bra that corresponds to ![]() . U00 is the Opposite Value in row 0, column 0 of the matrix. So U00|j^><j^| contributes U00 in the row 0, column 0 of the matrix.
. U00 is the Opposite Value in row 0, column 0 of the matrix. So U00|j^><j^| contributes U00 in the row 0, column 0 of the matrix.
Similarly, U01|j^><jv| corresponds to ![]() and contributes U01 in the row 0, column 1 of the matrix.
and contributes U01 in the row 0, column 1 of the matrix.
U10|jv><j^| ![]() contributes U10 in the row 1, column 0 of the matrix.
contributes U10 in the row 1, column 0 of the matrix.
U11|jv><jv| corresponds to ![]() and contributes U1 in the row 1, column of the matrix completing the matrix.
and contributes U1 in the row 1, column of the matrix completing the matrix.
Identity Gate
For example, write the identity gate ![]() as:
as:
- 1^|j^><j^| + 0|j^><jv| + 0|jv><j^| + 1^|jv><jv|
- = 1^|j^><j^| + 1^|jv><jv|
The values in the equations are in ket-bra format and each represents a 2*2 matrix, the sum of which gives the unitary matrix.
The ket-bra 1^|j^><j^| represents:
- 1^
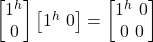
The ket-bra 0|j^><jv| represents:
- 0
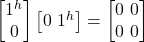
The ket-bra 0|jv><j^| represents:
- 0

The ket-bra 1|jv><jv| represents:
- 1^
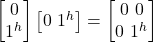
The sum of these four elements gives the identity gate
In U00, U01, U10 and U11, the subscript represents the Opposite Value in the row/column for that row/column. For example: The Opposite Value in the identity gate for U11 is 1^.
Pauli σx Gate
The matrix ![]() represents the unitary Pauli σx Gate.
represents the unitary Pauli σx Gate.
- So, Pauli σx = U00|j^><j^| + U01|j^><jv| + U10|jv><j^| + U11|jv><jv|
- => σx = 0|j^><j^| + 1^|j^><jv| + 1^|jv><j^| + 0|jv><jv|
- => σx = 1^|j^><jv| + 1^|jv><j^|
Next: Pauli and σf gates
Previous: Superposition

