September 8, 2024
Search
Search
Close this search box.

Quantum – Circuits – AH2

AH2 Gate 1/\sqrt{2} \begin {bmatrix} 1^h \ 0 \ 1^h\ 0\\ 0 \ 1^h \ 0\ 1^h\\ 1^h \ 0 \ 1^v\ 0\\ 0 \ 1^h \ 0\ 1^v \end{bmatrix}

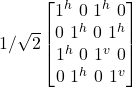
The quantum AH2 gate is the Haadmard gate for a multipart qubit with 2 qubits. The Haadamard operation, H, applies to the first qubit as follows:

  • AH2 |j^j^> =   1/\sqrt{2} \begin {bmatrix} 1^h \ 0 \ 1^h\ 0\\ 0 \ 1^h \ 0\ 1^h\\ 1^h \ 0 \ 1^v\ 0\\ 0 \ 1^h \ 0\ 1^v \end{bmatrix} * \begin {bmatrix} 1^h \\ 0 \\ 0\\ 0\end{bmatrix} = 1/\sqrt{2}\begin {bmatrix} 1^h \\ 0 \\ 1^h\\ 0\end{bmatrix} 
    • = 1/√2 (|j^j^> + |jvj^>)

  • Note that all gates are unitary. So, the quantum AH2 gate is reversible.
    • So, AH2 1/√2 (|j^j^> + |jvj^>) = 1/\sqrt{2} \begin {bmatrix} 1^h \ 0 \ 1^h\ 0\\ 0 \ 1^h \ 0\ 1^h\\ 1^h \ 0 \ 1^v\ 0\\ 0 \ 1^h \ 0\ 1^v \end{bmatrix} * 1/\sqrt{2}\begin {bmatrix} 1^h \\ 0 \\ 1^h\\ 0\end{bmatrix} = 1/2\begin {bmatrix} 2^h \\ 0 \\ 0\\ 0\end{bmatrix} = \begin {bmatrix} 1^h \\ 0 \\ 0\\ 0\end{bmatrix}
      • = |j^j^>

  • AH2 |jvj^> =   1/\sqrt{2} \begin {bmatrix} 1^h \ 0 \ 1^h\ 0\\ 0 \ 1^h \ 0\ 1^h\\ 1^h \ 0 \ 1^v\ 0\\ 0 \ 1^h \ 0\ 1^v \end{bmatrix} * \begin {bmatrix} 0 \\ 0 \\ 1^h\\ 0\end{bmatrix} = 1/\sqrt{2}\begin {bmatrix} 1^h \\ 0 \\ 1^v\\ 0\end{bmatrix} 
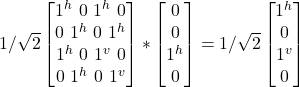
    • = 1/√2 (|j^j^> + –|jvj^>)

  • Note that all gates are unitary. So, the quantum AH2 gate is reversible.
    • So, AH2 1/√2 (|j^j^> + –|jvj^>) =   1/\sqrt{2} \begin {bmatrix} 1^h \ 0 \ 1^h\ 0\\ 0 \ 1^h \ 0\ 1^h\\ 1^h \ 0 \ 1^v\ 0\\ 0 \ 1^h \ 0\ 1^v \end{bmatrix} * 1/\sqrt{2}\begin {bmatrix} 1^h \\ 0 \\ 1^v\\ 0\end{bmatrix} = 1/2\begin {bmatrix} 0 \\ 0 \\ 2^h\\ 0\end{bmatrix} = \begin {bmatrix} 0 \\ 0 \\ 1^h\\ 0\end{bmatrix}
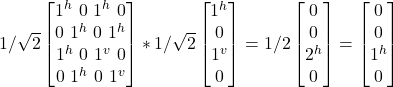
    • = |jvj^> 

Next: CZ gate

Previous: CNOT gate

Share to:

Leave a Reply

Your email address will not be published. Required fields are marked *