This post provides an example of a rotation chain involving three consecutive rotations. It uses the Wave Number Rotation formula adapted from Rodrigues’ formula and shows the Quaternion equivalent.
Wave Number Rotation Formula
![]()
Example 3
Rotation 1
In this example, 3 rotations take place one after the other:
- Rotation 1:

- Rotation 2:
 (Result of Rotation 1)
(Result of Rotation 1) - Rotation 3:
 (Result of Rotation 2)
(Result of Rotation 2)
Calculate the chain of rotations using the Wave Number ![]() formula.
formula.
Rotation 1:
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = ^-0.817\left[ \begin{array} {c} 0.408\hat{ } \\ 0.817 i\hat{ } \\ 0.408j\hat{ } \end{array} \right] + 0.866(\left[ \begin{array} {c} 1.225 \hat{ } \\ 0.816 i^v \\ 0.409j\hat{ } \end{array} \right]) + ^-0.5(\left[ \begin{array} {c} 1.225 \hat{ } \\ 0.816 i^v \\ 0.409j\hat{ } \end{array} \right] \times \left[ \begin{array} {c} 0.408 \hat{ } \\ 0.817 i\hat{ } \\ 0.408j\hat{ } \end{array} \right])\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-1b7b89e7b1452ecbcaa4d3fb7e4cccf6_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = \left[ \begin{array} {c} 0.333 ^v \\ 0.667 i^v \\ 0.333j^v \end{array} \right] + \left[ \begin{array} {c} 1.061 \hat{ } \\ 0.707 i^v \\ 0.354j\hat{ } \end{array} \right] + \left[ \begin{array} {c} 0.331\hat{ } \\ 0.3167i\hat{ }\\ 0.667j^v \end{array} \right]\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-4476bc3335489e6055f4d6e91fd75799_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = \left[ \begin{array} {c} 1.06 \hat{ } \\ 1.21 i^v \\ 0.65j^v \end{array} \right]\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-bfce6b611d0396a78e6de22b83820a07_l3.png)
Rotation 2:
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = ^-0.880\left[ \begin{array} {c} 0.267\hat{ } \\ 0.535 i\hat{ } \\ 0.802j\hat{ } \end{array} \right] + 0.707(\left[ \begin{array} {c} 0.622 \hat{ } \\ 1.023 i\hat{ } \\ 0.89j^v \end{array} \right]) + 0.707(\left[ \begin{array} {c} 0.622 \hat{ } \\ 1.023 i\hat{ } \\ 0.89j^v \end{array} \right] \times \left[ \begin{array} {c} 0.267 \hat{ } \\ 0.535 i\hat{ } \\ 0.802j\hat{ } \end{array} \right])\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-544251f7420a24583950ba91aa742fc5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = \left[ \begin{array} {c} 0.235 ^v \\ 0.471 i^v \\ 0.706j^v \end{array} \right] + \left[ \begin{array} {c} 0.44 \hat{ } \\ 0.724 i\hat{ } \\ 0.629j^v \end{array} \right] + \left[ \begin{array} {c} 0.917\hat{ } \\ 0.521i^v\\ 0.043j\hat{ } \end{array} \right]\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-cef3d6c756bdf191f10cd0aa3e0b0b8d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = \left[ \begin{array} {c} 1.12 \hat{ } \\ 0.27 i^v \\ 1.3j^v \end{array} \right]\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-fe8c3b239bf8ea0104b31a2fcdbe95f0_l3.png)
Rotation 3:
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\setlength\arraycolsep{2pt}v_{rot} = ^-0.525\left[ \begin{array} {c} 0.456 \hat{ } \\ 0.57 i\hat{ } \\ 0.684j\hat{ } \end{array} \right] + 0.866(\left[ \begin{array} {c} 0.553^v \\ 1.357 i\hat{ } \\ 0.762j^v \end{array} \right]) + 0.5(\left[ \begin{array} {c} 0.553^v \\ 1.357 i\hat{ } \\ 0.762j^v \end{array} \right] \times \left[ \begin{array} {c} 0.456 \hat{ } \\ 0.57 i\hat{ } \\ 0.684j\hat{ } \end{array} \right])\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-a45a6a9aa1baf8a846771c690815b6e7_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = \left[ \begin{array} {c} 0.239 ^v \\ 0.299 i^v \\ 0.359j^v \end{array} \right] + \left[ \begin{array} {c} 0.479^v \\ 1.175 i\hat{ } \\ 0.66j^v \end{array} \right] + \left[ \begin{array} {c} 0.681\hat{ } \\ 0.015i\hat{ }\\ 0.467j^v \end{array} \right]\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-22e1f7c304745d083f64ba223ebeff1a_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}v_{rot} = \left[ \begin{array} {c} 0.037^v \\ 0.891 i\hat{ } \\ 1.485j^v \end{array} \right]\end{equation*}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-5fea43f65c638ba56bb4de2ed04bd1fe_l3.png)
Equivalent R3 Rotation
Using the Vector Rotation functionality of the Omni Quaternion Calculator for an equivalent chain of rotations in ![]() , results as follows:
, results as follows:
-
Rotation 1:
 rotated by
rotated by  around
around  moves to
moves to 
-
Rotation 2:
 rotated by
rotated by  around
around  moves to
moves to 
-
Rotation 3:
 rotated by
rotated by  around
around 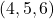 moves to
moves to 
This matches the Wave Number rotation result obtained above.
Equivalent Quaternion Rotation
Setting up Quaternion Equations
The following describes the Quaternion equivalent of this chain of Wave Number rotations:
- Rotation 1: Rotate
 by
by  around
around 
- Rotation 2: Rotate the result of rotation 1 by
 around
around 
- Rotation 3: Rotate the result of rotation 2 by
 around
around 
The unit vectors of the axes of rotation are:
- Rotation 1:
- Rotation 2:
- Rotation 3:
The Quaternions of Rotations are:
Rotation 1: ![]()
Rotation 2: ![]()
Rotation 3: ![]()
Performing Quaternion Equations
The quaternion of rotation, ![]() rotates the quaternion vector,
rotates the quaternion vector, ![]() as follows:
as follows:
![]() rotates the result of the first rotation:
rotates the result of the first rotation:
![]() rotates the result of the second rotation:
rotates the result of the second rotation:
Completing the Quaternion Sandwich
The Quaternion sandwich needs to be completed to obtain a result in ![]() . Consequently, the result so far needs to be multiplied by the conjugate of the three rotations
. Consequently, the result so far needs to be multiplied by the conjugate of the three rotations ![]() .
.
- The product of the three rotations is

- Therefore the conjugate of the three rotations is

- Giving the product of the result so far and the conjugate as

The result matches the Wave Numbers outcome of ![]() , allowing for minor rounding differences due to the number of multiplications.
, allowing for minor rounding differences due to the number of multiplications.
Next: Comparing Wave Number and Quaternion Efficiency
Previous: Complex Rotation Example 2

