Quantum – Theory – Basis & Born’s Rule

This post describes Born’s rule that defines the probability of the collapse of qubits to a quantum basis.

z-axis Basis

Define the z-axis basis states, {|j^{^}>, |j^v>},  as:

• |jˆ> = 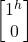 and |j^v> =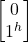

which are orthogonal because their inner product = 0:

               <j^{^}|j^v> = [1^{^} 0].   = 1^{^}*0 + 0*1^{^} = 0

Born’s Rule

In Wave Numbers, express probability as a Counter as it is a magnitude. Born’s rule states that the probability that a state |ψ> collapses when measured onto the basis {|x>, |x┴>}   (x and its orthogonal complement)  is: 

• P(x) = |<x|ψ>|²  and ∑P(xi) = 1

In other words, the probability of the state <x| is the square of the dot product of <x| and |ψ>. The sum of all probabilities = 1.

The probability of the qubit measuring as |j^{^}> or |j^v> depends on the state equation. Given a state equation of |ψ> =  a + bi, then the probability of  |j^{^}> is  a² and the probability of |j^v> is b² and a² + b² = 1.

The top row of the matrix that represents a state gives the probability of the qubit measuring as |j^{^}> and the bottom the probability of the qubit measuring as |j^v>.

So, represents a 100% chance of the qubit being a |j^{^}>  and  a 100% chance of it measuring as |j^v>.  

1/√2 represents a 50% chance of either the qubit measuring as |j^{^}> or |j^v>.

also represents a 100% chance of the qubit being a |j^{^}> and   a 100% chance of it measuring as |j^v>.

1/√2 , 1/√2  and   1/√2represent a 50% chance of either the qubit measuring as |j^{^}>   or |j^v>  .

Examples

For the state |ψ> = |j^{^}> = Born’s rule implies:

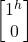• P(|j^{^}>) = |(1^{^} 0]. |²
• = |1^{^}*1^{^} + 0*0)|² = 1

Secondly, for the state |ψ> = 1/√3(|j^{^}> + √2|j^v>) = 1/√3 Born’s rule implies:

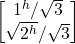• P(|j^{^}>) = |[1^{^} 0]. |²
• = |1^/√3  + 0 )|²  = 1/3
• => P(j^v) = 2/3

Thirdly, for the state example: |ψ> = 1/√2(|j^{^}>  + ^–|j^v>) = 1/√2 Born’s rule implies:

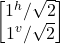• P(|j^{^}>) = |[1^{^} 0]. |²
• = |1^{^}/√2  + 0*√2^v )|²  = 1/2
• => P(j^v) = 1^{^}/2

x-axis Basis and Born’s Rule

In Wave Numbers, define the x-axis basis states, {|^{^}>, |^v> }, as:            

• |^{^}> = (|jˆ> + |j^v>)/√2  =   

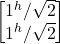
• |^v> = (|jˆ> + ^–|j^v>)/√2  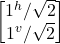=   which are orthogonal because the inner product of their bra-ket is 0:
  • <^{^}|^v> = [1^{^}/√2^{^} 1^/√2].  
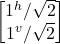
    • = 1^{^}/√2*1^{^}/√2 + 1^{^}/√2*1^v/√2
    • = 1^{^}/2 +  1^v/2 = 0

Example

For the state |ψ> = (|j^{^}>  + ^–|j^v>)/√2 = 1/√2    (The state |^v>)

• P(|^{^}>) = |[1^{^}/√2 1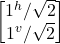^{^}/√2].  |²
• = |(1^{^}/√2)*(1^{^}/√2)  + (1^{^}/√2)*(1^v/√2)|²
• = | 1^{^}/2 + 1^v/2|  = 0

This makes sense as |ψ> is |^v>  and the probability of the qubit being |^{^}> is 0.

y-axis Basis and Born’s Rule

Defined the y-axis basis states, {|i^{^}>, |i^v> }, as:

• |i^{^}> = (|jˆ> + iˆ|j^v>)/√2 =    

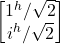
• |i^v> = (|jˆ> + i^v|j^v>)/√2 = 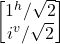    which are orthogonal because the inner product of their bra-ket is 0:
  • <i^{^}|i^v> = [1^{^}/√2 i^v/√2]. 
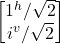
    • = 1^{^}/√2*1^{^}/√2 + i^v/√2*i^v/√2
    • = 1^{^}/2  + 1^v/2        = 0

Note that changing |i^{^}> to <i^{^}|results in the Opposite Sign of i being flipped as shown in earlier post on bra-kets.

Example

For |ψ> = (|j^{^}>  + iˆ|j^v>)/√2 = 1/√2    (The state |i^{^}>)

• P(|i^{^}>) = |[1^{^}/√2 i^v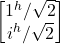/√2].  |²
• = |(1^{^}/√2)*(1^{^}/√2)  + (i^v/√2)*(i^{^}/√2)|²
• = | 1^{^}/2 + 1^{^}/2|  = 1

Note that changing |i^{^}> to <i^{^}|results in the Opposite Sign of i being flipped as shown in earlier post on bra-kets.

This makes sense as |ψ> is |i^{^}>  and the probability of the qubit |i^{^}> is 1.

Next: Single and Multipart Qubits

Previous: Bra-Kets