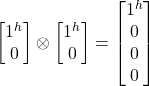Quantum – Theory – Matrices

Introduction

Wave Number matrices allow for the addition and multiplication of quantum states. Opposite Values and flipping work together to get differences and consequently eliminate the need for subtraction. As in classical maths, there is no such thing as division with matrices. Multiply matrix a by the inverse of matrix b in order to divide matrix a by matrix b,

The transpose function rotates a matrix so that the rows become the columns and vice versa.

Addition

Note that the result of each addition is given after normalisation.

$\begin {bmatrix} 1^h \\ 0 \end{bmatrix} + \begin {bmatrix} 1^v \\ 0 \end{bmatrix} = \begin {bmatrix} 0 \\ 0 \end{bmatrix}$

$\begin {bmatrix} 1^h \\ 0 \end{bmatrix}+\begin {bmatrix} 1^h \\ 0 \end{bmatrix}=2\begin {bmatrix} 1^h \\ 0 \end{bmatrix}=\begin {bmatrix} 1^h \\ 0 \end{bmatrix}$

$\begin {bmatrix} 1^v \\ 0 \end{bmatrix} + \begin {bmatrix} 1^v \\ 0 \end{bmatrix} = 2\begin {bmatrix} 1^v \\ 0 \end{bmatrix} = \begin {bmatrix} 1^v \\ 0 \end{bmatrix}$

$\begin {bmatrix} 0 \\ 1^h \end{bmatrix} + \begin {bmatrix} 0 \\ 1^v \end{bmatrix} = \begin {bmatrix} 0 \\ 0 \end{bmatrix}$

$\begin {bmatrix} 0 \\ 1^h \end{bmatrix} + \begin {bmatrix} 0 \\ 1^h \end{bmatrix} = 2\begin {bmatrix} 0 \\ 1^h \end{bmatrix} = \begin {bmatrix} 0 \\ 1^h \end{bmatrix}$

$\begin {bmatrix} 0 \\ 1^v \end{bmatrix}+ \begin {bmatrix} 0 \\ 1^v\end{bmatrix}=2\begin {bmatrix} 0 \\ 1^v \end{bmatrix}=\begin {bmatrix} 0 \\ 1^v \end{bmatrix}$

$\begin {bmatrix} i^h \\ 0 \end{bmatrix} + \begin {bmatrix} i^v \\ 0 \end{bmatrix} = \begin {bmatrix} 0 \\ 0 \end{bmatrix}$

$\begin {bmatrix} i^h \\ 0 \end{bmatrix} + \begin {bmatrix} i^h \\ 0 \end{bmatrix} = 2\begin {bmatrix} i^h \\ 0 \end{bmatrix} = \begin {bmatrix} i^h \\ 0 \end{bmatrix}$

$\begin {bmatrix} i^v \\ 0 \end{bmatrix} + \begin {bmatrix} i^v \\ 0\end{bmatrix} = 2\begin {bmatrix} i^v \\ 0 \end{bmatrix} = \begin {bmatrix} i^v \\ 0 \end{bmatrix}$

$1/\sqrt{2} \begin {bmatrix} i^v \\ 1^h \end{bmatrix} + 1/\sqrt{2} \begin {bmatrix} 1^h \\ i^v \end{bmatrix} = 1/\sqrt{2} \begin {bmatrix} 1^h +i^v \\ 1^h + i^v \end{bmatrix}$

$1/\sqrt{2} \begin {bmatrix} i^v \\ 1^v \end{bmatrix} + 1/\sqrt{2} \begin {bmatrix} 1^v \\ i^v\end{bmatrix} = 1/\sqrt{2}\begin {bmatrix} 1^v + i^v \\ 1^v + i^v \end{bmatrix}$

$1/\sqrt{2} \begin {bmatrix} 1^h \\ i^v \end{bmatrix} + 1/\sqrt{2} \begin {bmatrix} 1^v \\ i^h \end{bmatrix} = \begin {bmatrix} 0 \\ 0 \end{bmatrix}$

$1/\sqrt{2} \begin {bmatrix} 1^h \\ i^h \end{bmatrix} + 1/\sqrt{2} \begin {bmatrix} 1^h \\ i^h \end{bmatrix} = 2/\sqrt{2}\begin {bmatrix} 1^h \\ i^h \end{bmatrix} = 1/\sqrt{2}\begin {bmatrix} 1^h \\i^h \end{bmatrix}$

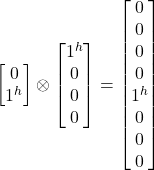
Multiplication

Multiply single and multipart qubits together using the tensor product. Note that the symbol $\otimes$ represents the tensor product operation.

The multipart qubit |j^vj^{^}j^{^}> can be represented in a matrix. To do this, calculate the tensor product of the qubits starting from the rightmost multiplication in the multipart qubit which in this case is j^{^}j^{^}.

- $\begin {bmatrix} 1^h \\ 0 \end{bmatrix}\otimes \begin {bmatrix} 1^h \\ 0 \end{bmatrix} = \begin {bmatrix} 1^h \\ 0 \\ 0 \\ 0 \end{bmatrix}$

Finally multiply the result by the last qubit in the multipart qubit. i.e. j^v.

- $\begin {bmatrix} 0 \\ 1^h \end{bmatrix}\otimes \begin {bmatrix} 1^h \\ 0 \\ 0 \\ 0 \end{bmatrix} = \begin {bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1^h \\ 0 \\ 0 \\ 0 \end{bmatrix}$

Next: Superposition

Previous: Single and Multipart Qubits

Share to:

Quantum – Theory – Matrices

Introduction

Addition

Multiplication

Leave a Reply Cancel reply