This post shows how R2 Wave Numbers are used with Pauli gates. It also introduces the σf gate which flips the Opposite Signs of both bits of a qubit.
Pauli σx Gate 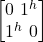
The purpose of the Pauli σx gate is to bit-flip a qubit. It does this by inverting the bits up and down in the matrix. It is also known as the x-gate or the Not Gate. The σx gate is a rotation around the x axis by 180o. For example: The state |j^> becomes |jv>. In this case the electron changes to the |jv> state and has been rotated 180o around the x-axis.
Basis States
- σx |j^> =
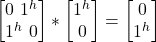 = |jv>
= |jv>
- σx |jv> =
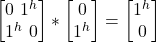 = |j^>
= |j^>- Note that all gates are unitary and as such reversible. So, σx |j^> followed by σx |jv> returns the state to |j^>
- σx –|j^> =
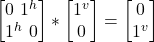 = –|jv>
= –|jv>
- σx –|jv> =
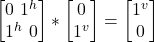 = –|j^>
= –|j^>
States in Superposition
- σx
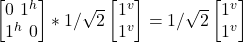
- σx
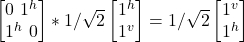
- σx
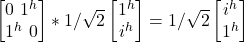
- σx
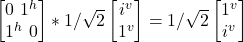
- σx
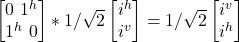
σx Gate in Dirac Notation
- σx |jv > =(|j^><jv| + |jv><j^|)*|jv>
- = |j^><jv|jv> + |jv><j^|jv>
- = |j^>1 + |j^>0
- Note that bra-kets used for resolving
- <jv|jv> = 1 and <j^|jv> = 0.
- Note that bra-kets used for resolving
- = |j^>
Pauli σz Gate 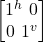
The purpose of the Pauli σz gate is to phase-flip a qubit. It does this by changing the Opposite Sign of the second bit only. It is also known as the z-gate. This is a 180o rotation around the z-axis. For example: The state |jv> becomes –|jv>. In this case the electron stays at the same location but it has been rotated 180o around the z-axis.
Basis States
- σz |j^> =
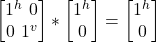 = |j^>
= |j^>
- σz –|j^> =
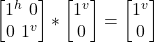 = –|j^>
= –|j^>
- σz |jv> =
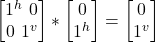 = –|jv>
= –|jv>
- σz –|jv> =
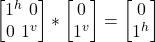 = |jv>
= |jv>- Note that all gates are unitary and as such reversible. So, σz |jv> followed by σz –|jv> returns the state to |jv>
States in Superposition
- σz
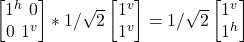
- σz
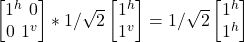
- σz
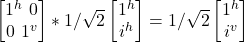
- σz
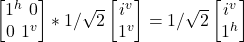
- σz
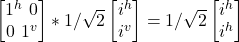
σz Gate in Dirac Notation
- σz |jv > =(|j^><j^| + –|jv><jv|)*|jv>
- = |j^><j^|jv> + –|jv><jv|jv>
- = |j^>0 + –|jv>1
- Note that bra-kets used for resolving
- <j^|jv> = 0 and <jv|jv> = 1.
- Note that bra-kets used for resolving
- =–|jv>
Pauli σy Gate 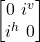
The purpose of the Pauli σy gate is to bit-flip and phase-flip a qubit. It is also known as the y-gate. The phase-flip is different to σz as it can introduce i to the first and second bits of the qubit. It is similar σz because it does change the Opposite Sign of the second bit.
For example: The state |j^> becomes i|jv> in the first example below. In this case the electron changes to the i|jv> state, has been rotated 180o around the y-axis. The operation also introduces i. Note that it changes the Opposite Sign of the second bit only, so not in this example.
Another example: The state |jv> becomes –i|j^> in the fourth example below. In this case the electron changes to the –i|j^> state, has been rotated 180o around the y-axis. Note that it changes the Opposite Sign of the second bit before flipping.
Basis States
- σy |j^> =
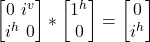 = i|jv>
= i|jv>
- σy i|jv> =
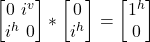 = |j^>
= |j^>- Note that all gates are unitary and as such reversible. So, σy |j^> followed by σy |jv> returns the state to |j^>
- σy –|j^> =
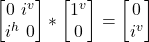 = –i|jv>
= –i|jv>
- σy |jv> =
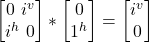 = –i|j^>
= –i|j^>
- σy –|jv> =
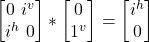 = i|j^>
= i|j^>
States in Superposition
- σy
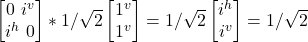 (i|j^> + –i|jv>)
(i|j^> + –i|jv>)
- σy
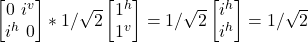 (i|j^> + i|jv>)
(i|j^> + i|jv>)
- σy
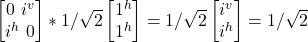 –i|j^> + i|jv>
–i|j^> + i|jv>
- σy
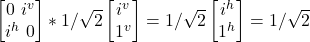 (i|j^> + |jv>)
(i|j^> + |jv>)
- σy
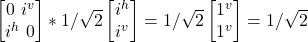 (–|j^> + –|jv>)
(–|j^> + –|jv>)
σy Gate in Dirac Notation
- σy |jv > =(–i|j^><jv| + i|jv><j^|)*|jv>
- = –i|j^><jv|jv> + i|jv><j^|jv>
- = –i|j^>+ i|jv>0
- Note that bra-kets used for resolving
- <jv|jv> = 1 and <j^|jv> = 0
- Note that bra-kets used for resolving
- =–i|j^>
σf Gate 
A new gate has been introduced to Wave Numbers similar to the Pauli gates. The σf gate was created in order to be able to Flip the Opposite Signs of both bits. It can also be called the f-gate.
Basis States
- σf |j^> =
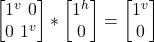 = –|j^>
= –|j^>
- σf –|j^> =
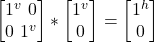 = |j^>
= |j^>- Note that all gates are unitary and as such reversible. So, σf |j^> followed by σf |jv> returns the state to |j^>
- σf |jv> =
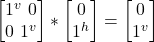 = –|jv>
= –|jv>
- σf –|jv> =
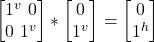 = |jv>
= |jv>
States in Superposition
- σf
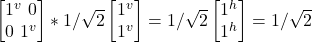 (|j^> + |jv>)
(|j^> + |jv>)
- σf
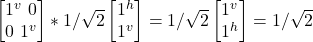 (–|j^> + |jv>)
(–|j^> + |jv>)
- σf
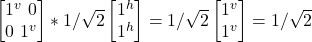 (–|j^>+ –|jv>)
(–|j^>+ –|jv>)
- σf
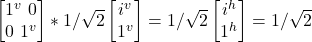 (i|j^> + |jv>)
(i|j^> + |jv>)
- σf
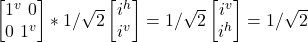 (–i|j^> + i|jv>)
(–i|j^> + i|jv>)
σf Gate in Dirac Notation
- σf |j^> =(–|j^><j^| + –|jv><jv|)*|j^>
- = –|j^><j^|j^> + –|jv><jv|j^>
- = –|j^>1 + –|jv>0
- Note that bra-kets used for resolving
- <j^|j^> = 1 and <jv|j^> = 0
- Note that bra-kets used for resolving
- = –|j^>
Next: Haadamard Gate
Previous: Introduction

