Orthogonal Rule
The layout of the R3 axes is defined as part of the Wave Number axioms. The Axioms of Rotation provide the Orthogonal rule which states that multiplication by a unitary is the equivalent of rotation around the unitary’s axis by 90o. This allows for the derivation of the R3 unitary multiplication table, shown below, from rotations on the sphere. Check this out using the Wave Number Rotation Ball.
R3 Multiplication Table
| * | 1^ | 1v | i^ | iv | j^ | jv |
| 1^ | 1^ | 1v | j^ | jv | iv | i^ |
| 1v | 1^ | 1v | jv | j^ | i^ | iv |
| i^ | jv | j^ | i^ | iv | 1^ | 1v |
| iv | j^ | jv | i^ | iv | 1v | 1^ |
| j^ | i^ | iv | 1v | 1^ | j^ | jv |
| jv | iv | i^ | 1^ | 1v | j^ | jv |
Algebra and Comparison with R1 and R2
During R3 rotation, as represented by unitary multiplication, the axis of rotation is that of the Operator. For example: in the multiplication of 1^*i^, the point at i^ rotates by 90^o around the x-axis to the point j^ on the z-axis. When a point rotates on its own axis, it stays exactly where it is. This leads to the result that 1^*1^ = 1^ and 1^*1v = 1v. Interestingly 1v*1v = 1v and 1v*1^ = 1^ in R3 rotation. This is because the rotation is on its own axis, the x-axis. This differs from R1 and R2 where multiplying by 1v reverses the Opposite Sign because the axis of rotation is different. R3 allows a type of rotation not available to R1 and R2. Check out all these rotations on the Wave Numbers Rotation ball and with the Wave Number Calculator.
Where points rotate on their own axes, consider it as the orientation of the point changing even though the point stays at the same location. Of course a point does not take up any space and so does not have an orientation.
R1, R2 and R3 Tables
The R1 table is a subset of the R2 table. However, the R2 table is not a subset of R3. In R3 each point now has five alternative points to move to as opposed to three in R2. A rotation of 90o from a point in R2 will reach a different neighbour than in R3. For example: 90^o counterclockwise of 1^ around the origin in R2 brings you to i^. 90^o counterclockwise from 1^ in R3 brings you to jv around the y-axis and to i^ around the z-axis. A 90^o rotation is not possible in R1, so you can only ever get to and from 1^ and 1v.
Comparison with Quaternions
The table below is the quaternion multiplication table. The leftmost column indicates the multiplier, while the topmost row represents the multiplicand.
To interpret the quaternion table, consider ![]() . This means that multiplying
. This means that multiplying ![]() by
by ![]() results in
results in ![]() . Here,
. Here, ![]() denotes a rotation around the x-axis. Similarly,
denotes a rotation around the x-axis. Similarly, ![]() signifies that multiplying
signifies that multiplying ![]() by
by ![]() yields
yields ![]() . Rotating
. Rotating ![]() or
or ![]() by themselves results in
by themselves results in ![]() , which is a scalar. Finally, multiplying the scalar
, which is a scalar. Finally, multiplying the scalar ![]() by
by ![]() remains
remains ![]() .
.
| * | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
The entries in the rows of the R3 multiplication table can be directly compared to those in the quaternion table.
In the R3 system, there is no equivalent of the scalar ![]() . Instead,
. Instead, ![]() and
and ![]() correspond to the quaternion values
correspond to the quaternion values ![]() and
and ![]() respectively. Row i of the quaternion table is compared with its equivalent Wave Number, row
respectively. Row i of the quaternion table is compared with its equivalent Wave Number, row ![]() . Quaternion values such as
. Quaternion values such as ![]() are calculated as the result of
are calculated as the result of ![]() .
.
Row Comparison with Quaternions for R3’s a = 1^ and Quaternion a = i:
- Quaternions:
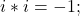 Wave Numbers:
Wave Numbers: 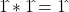
- Quaternions:
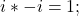 Wave Numbers:
Wave Numbers: 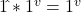
- Quaternions:
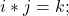 Wave Numbers:
Wave Numbers: 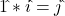
- Quaternions:
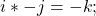 Wave Numbers:
Wave Numbers: 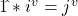
- Quaternions:
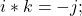 Wave Numbers:
Wave Numbers: 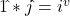
- Quaternions:
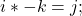 Wave Numbers:
Wave Numbers: 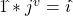
The results between the quaternion and Wave Number multiplication tables largely correspond. The primary differences arise from the absence of a scalar multiplier or result in the Wave Number system. For instance, in quaternions, ![]() , whereas in the R3 system,
, whereas in the R3 system, ![]() . Similarly, multiplying
. Similarly, multiplying ![]() . In both cases, the Wave Number R3 multiplications leave the operand unchanged.
. In both cases, the Wave Number R3 multiplications leave the operand unchanged.
Next: Universal Rules of Rotation
Previous: Simple Examples

