R3 – Rotation – Spherical Coordinates

This post covers the formula for spherical coordinates in R3. Examples of rotation using the formula are given.

Cartesian Coordinates

The Cartesian coordinates of a point are based on the intersection of perpendicular lines from the point with the x, y and z-axes. For example: the Cartesian coordinates at a point on the surface of the unit sphere equidistant from (1^{^},0, 0), (0, i^{^}, 0) and (0, 0, j^{^}) is (0.577^{^}, 0.577i^{^}, 0.577j^{^}). Check it out on the Wave Number Rotation Ball.

All Opposite Values on axes are real, so there is no need for the association of Cartesian coordinates with imaginary numbers as in classical maths.

Spherical Coordinates

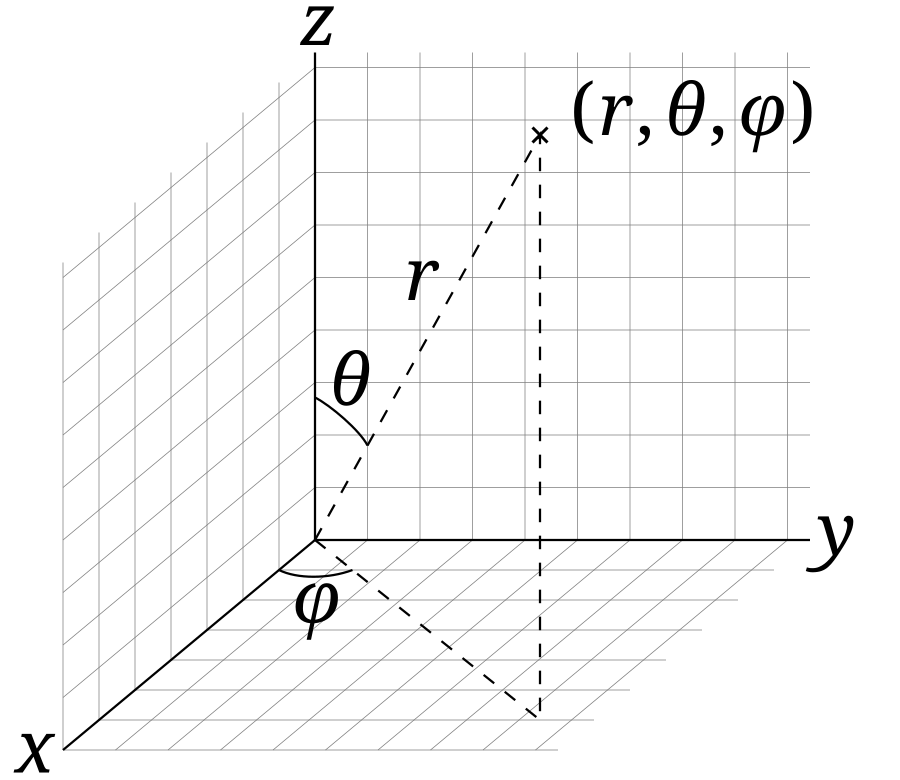
https://upload.wikimedia.org/wikipedia/commons/4/4f/3D_Spherical.svg

The spherical coordinate system uses 3 elements. First, there is the radius or distance from the origin, r, which is a magnitude only, a Counter. 

The second is the angle down from the z-axis to the point represented by an Opposite Value, the polar angle or phi φ (Note vertical line to remind its polar). The polar angle cannot be greater than 180^{^o} no matter what the Opposite Value of the point.

Third is the azimuth or horizontal angle or theta, θ (Note horizontal line to remind it is horizontal). The projection of the Opposite Value onto the x-y plane forms a line with the origin. It is the angle between this line and the x-axis that is the azimuth angle. It is measured counterclockwise from the x-axis and can be up to 360^{^o}. For example: (0, i^{^},0) is π^{^}/2 from the x-axis.

In R3, Sines and Cosines are based on the unit circle and Counters are used. For example cos(0) = 1, sin(0) = 0, and cos(π^{^}) = ^–1, sin(π^{^}) = 0, cos(2π^{^}/3) = -1/2  , sin(π^{^}/2) = 1,  cos(π^{^}/3) = √3/2, sin(π^v/2) = ^–1,  cos(π^v/3) = ^–√3/2.

The spherical coordinates system defines coordinates as:

• x = r*sin(φ)*cos(θ)*1^{^}
• y = r*sin(φ)*sin(θ)*i^{^}
• z = r*cos(φ)*j^{^}

Examples

Axes Points

Calculate the R3 spherical coordinates of the following points on the x, y and z-axes using the radius – r, the polar angle down from the z-axis – φ and the horizontal angle from the x-axis – θ.

• Take the case of a point at (1^{^}, 0, 0), r = 1, φ = π^{^}/2 and θ = 0
  • x = r*sin(π^{^}/2)*cos(0)*1^{^} = 1*1*1^{^} = 1^{^}
  • y = r*sin(π^{^}/2)*sin(0)*i^{^} = 1*0*i^{^} = 0
  • z = r*cos(π^{^}/2)*j^{^} = 1*0*j^{^} = 0

• Take the case of a point at (0, i^{^}, 0), r = 1, φ = π^{^}/2 and θ = π^{^}/2
  • x = r*sin(π^{^}/2)*cos(π^{^}/2)*1^{^} = 1*0*1^{^} = 0
  • y = r*sin(π^{^}/2)*sin(π^{^}/2)*i^{^} = 1*1*i^{^} = i^{^}
  • z = r*cos(π^{^}/2)*j^{^} = 1*0*j^{^} = 0

• Take the case of a point at (0, 0, j^{^}), r = 1, φ = 0 and θ= 0
  • x = r*sin(0)*cos(0)*1^{^} = 0*1*1^{^} = 0
  • y = r*sin(0)*sin(0)*i^{^} = 0*0*i^{^} = 0
  • z = r*cos(0)*j^{^} = 1*1*j^{^}= j^{^}

• Take the case of a point (0, 0, j^v), r = 1, φ = π^{^} and θ= 0
  • x = r*sin(π^{^})*cos(0)*1^{^} = 0*1*1^{^} = 0
  • y = r*sin(π^{^})*sin(0)*i^{^} = 0*0*i^{^} = 0
  • z =r* cos(π^{^})*j^{^} = 1*^–1*j^{^}= j^v

Some Other Points

Calculate the R3 spherical coordinates of some points not on the main axes.

• Take the case of a point with a radius of 1.73, φ = 54.7^{^o} and θ = 45^{^o}
  • x = r*sin(φ)*cos(θ)*1^{^} 
    • 1.73*sin(54.7^{^o})*cos(45^{^o})*1^{^} = 1.73*0.817*0.707*1^{^} = 1^{^}
  • y = r.sin(φ).sin(θ).i^{^}  
    • 1.73*sin(54.7^{^o})*sin(45^{^o})*i^{^} = 1.73*0.817*0.707*i^{^} = i^{^}
  • z = r*cos(φ)*j^{^}            
    • 1.73*cos(54.7^{^o})*j^{^} = 1.73*0.577*j^{^} = j^{^}
  • Giving the point (1^{^}, i^{^}, j^{^})

• Take the case of a point with a radius of 1.73, φ = 125.26^{^o} and θ = 225^{^o}
  • x = r*sin(φ)*cos(θ)*1^{^} 
    • 1.73*sin(125.26^{^o})*cos(225^{^o})*1^{^} = 1.73*0.817*^–0.707*1^{^} = ^–1*1^{^} =1^v
  • y = r.sin(φ).sin(θ).i^{^}  
    • 1.73*sin(125.26^{^o})*sin(225^{^o})*i^{^} = 1.73*0.817^{^}*^–0.707*i^{^} = ^–1*i^{^} = i^v
  • z = r.cos(φ).j^{^}            
    • 1.73*cos(125.26^{^o})*j^{^} = 1.73*0.577^–*j^{^} = 1^–*j^{^} =j^v
  • Giving the point (1^v, i^v, j^v)

• Take the case of a point with a radius of 2 and φ = 150^{^o} and θ = 300^{^o}
  • x = r*sin(φ)*cos(θ)*1^{^} 
    • 2*sin(150^{^o})*cos(300^{^o})*1^{^} = 2*0.5*.5*1^{^} gives x = 0.5^{^}
  • y = r*sin(φ)*sin(θ)*i^{^}  
    • 2*sin(150^{^o})*sin(300^{^o})*i^{^} = 2*0.5*^–0.866*i^{^}= ^–0.866*i^{^} gives y = 0.866i^v
  • z = r*cos(φ)*j^{^}           
    • 2*cos(150^{^o})*j^{^} = 2*^–0.866*j^{^} = ^–1.73*j^{^} gives z = 1.73j^v
  • Giving the point (0.5^{^}, 0.87i^v, 1.73j^v)

Next: Hyperspherical Coordinates

Previous: Complex Rotations Example 3