R3 – Multiplication Use of Trigonometry

This post covers the use of trigonometry in R3 multiplication. It also describes a trigonometric formula for multiplication.

Finding the angles φx, φy and φz

R3 multiplication uses trigonometry when it uses the cosines of the angles φx, φy and φz in the multiplication formula later in this post. The following is a description of one method of finding the values of the angles.

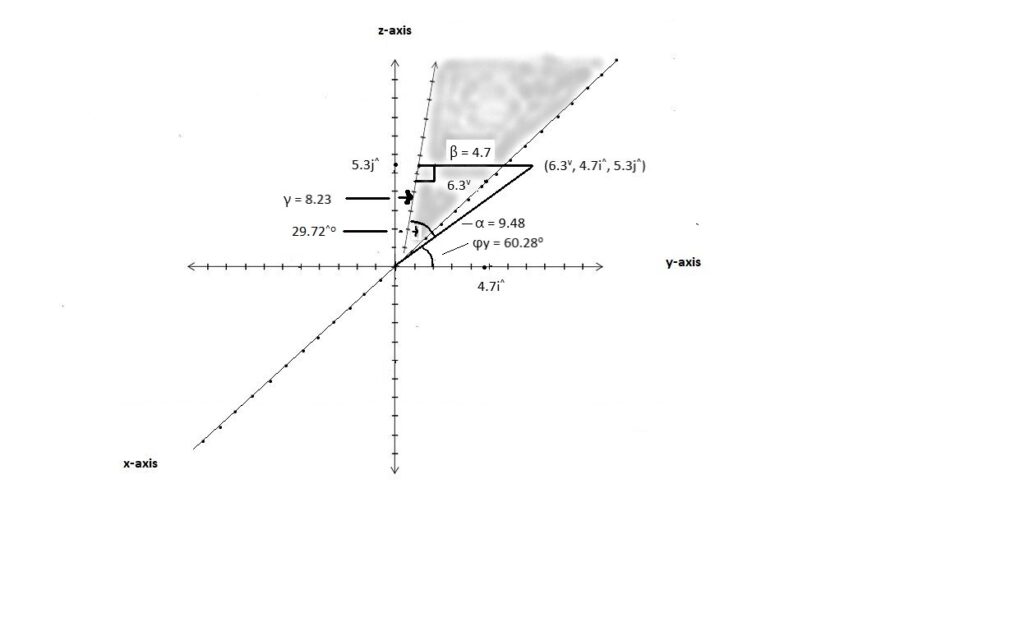
The distance R of any point (a, b, c) from the origin as given by Pythagoras’ theorem is R = √(|a|² + |b|² + |c²). The distance α of the point (6.3^v, 4.7i^{^}, 5.3j^{^}) from the origin is α =(√(|6.3|² + |4.7|²+ |5.3²) = 9.48. This is a Counter.

A line from (6.3^v, 4.7i^{^}, 5.3j^{^}) forms a right angle with the x-z plane (y=0). So, the x-z plane is shaded in the diagram above. The line to the plane has a magnitude of β = 4.7 which is the counter of the y-axis coordinate.

The magnitude of the third line of the triangle, calculated using Pythagoras’ theorem, is γ = 8.23. Note that this line runs from the point (6.3^v, 0, 5.3j^{^}) to (0, 0, 0). The 3 points of the triangle are (6.3^v, 4.7i^{^}, 5.3j^{^}), (6.3^v, 0, 5.3j^{^}) and (0, 0, 0). The angle between the lines (6.3^v, 4.7i^{^}, 5.3j^{^}) and (6.3^v, 0, 5.3j^{^}) is calculated from the sine of the angle. It is 4.7/9.48 = 0.496 which equates to 29.72^{^o}.

The angle formed by the line from (6.3^v, 4.7i^{^}, 5.3j^{^}) and the y-axis represented by (0, i^{^}, 0) is φy. This is an exterior angle to the triangle that equates to the second acute angle of the triangle. The cosine of φy is 4.7/9.48 = 0.496 which equates to 60.28^{^o}.

A line from (6.3^v, 4.7i^{^}, 5.3j^{^}) that forms a right angle with the y-z plane (x = 0) has a magnitude of β = ^–6.3, the x-axis coordinate. The angle formed by the line from (6.3^v, 4.7i^{^}, 5.3j^{^}) and the x-axis represented by (1^{^}, 0, 0) is φx. Calculate φx similarly to φy. Consequently, the cosine of φx is ^–6.3/9.48 = ^–0.665 which equates to 131.68^{^o}.

A line from (6.3^v, 4.7i^{^}, 5.3j^{^}) that forms a right angle with the x-y plane has a magnitude of β = 5.3, the z-axis coordinate. The angle formed by the line from (6.3^v, 4.7i^{^}, 5.3j^{^}) and the z-axis represented by (0, 0, j^{^}) is φz. Calculate φz similarly to φy. Consequently, the cosine of φz is 5.3/9.48 = 0.559 which equates to 56^{^o}.

Dot Product Approach to find φx, φy and φz

According to Wikipedia, ‘The basic feature of the dot product that connects it with Euclidean geometry is that it is related to both the length of a vector, denoted ‖x‖, and to the angle θ between two vectors x and y by means of the formula:

x ⋅ y = ||x|||y||cosφ’

The dot product of (6.3^v, 4.7i^{^}, 5.3j^{^}) and the y-axis at (0, i^{^}, 0) is the counter4.7 as explained in the post on dot products. This is the counter of the y coordinate which is the distance from the point (6.3^v, 4.7i^{^}, 5.3j^{^}) to the x-z plane as shaded in the diagram above. So,

4.7 = ||x|||y||cosφ => cosφ = 4.7/(||x|||y||)
- => cosφ = 4.7/(|√(|6.3|² + |4.7|²+ |5.3²)|)*(√(1² + 0² + 0²)
- => cosφ = 4.7/9.48
- = 0.496
- = 60.28^{^o} is φy

Similarly, find φx using the dot product of (6.3^v, 4.7i^{^}, 5.3j^{^}) with the x-axis, (^{^}, 0, 0) which = ^–6.3.

^–6.3 = ||x|||y||cosφ => cosφ = ^–6.3/(||x|||y||)
- => cosφ = ^–6.3/9.48
- = ^–0.665
- = 131.65^{^o} is φx.

Find φz using the dot product of (6.3^v, 4.7i^{^}, 5.3j^{^}) with the z-axis, (0, 0, j^{^}) which = 5.3.

5.3 = ||x|||y||cosφ => cosφ = 5.3/(||x|||y||)
- => cosφ = 5.3/9.48
- = 0.559
- = 56^{^o} is φz.

R3 Multiplication Geometric Formula

An alternative method to using the multiplication table for calculating multiplication is to use the following trigonometric multiplication formula. In R3 multiplication, it is necessary to multiply the magnitudes of the points and use trigonometric functions to account for the angles of the points.

The distance $R$ of any point $(x, y, z)$ from the origin as given by Pythagoras’ theorem is $R = \sqrt{(|x|^2 + |y|^2 + |z|^2)}$ .

Any point $(x, y, z)$ can be defined in terms of the angles φx, φy and φz as discussed above.

Given that $(Ax, Ay, Az) * (Bx, By, Bz) = (Cx, Cy, Cz)$ , the formula for calculating $(Cx, Cy, Cz)$ is:

$Cx =RA*RB(cos(\psi Ax)\hat{ }.cos(\psi Bx)\hat{ } + cos(\psi Ay)i\hat{ }.cos(\psi Bz)j\hat{ } + cos(\psi Az)j\hat{ }.cos(\psi By)i\hat{ })$
$Cy = RA*RB(cos(\psi Ax)\hat{ }.cos(\psi Bz)j\hat{ } + cos(\psi Ay)i\hat{ }.cos(\psi By)i\hat{ } + cos(\psi Az)j\hat{ }.cos(\psi Bx)\hat{ })$
$Cz = RA*RB(cos(\psi Ax)\hat{ }.cos(\psi By)i\hat{ } + cos(\psi Ay)i\hat{ }.cos(\psi Bx)\hat{ }+ cos(\psi Az)j\hat{ }.cos(\psi Bz)j\hat{ })$