R3 – Complex Rotations – Example 2

This post gives a second example of a complex R3 rotation. It uses the Wave Number Rotation formula adapted from Rodrigues’ formula and shows the Quaternion equivalent.

Wave Number Rotation Formula

$v_{rot} = (u_r \cdot v)u_r + sin\theta(u_r \times v) +cos\theta((u_r \times v)\times u_r)$

Example 2

Take for example the rotation of 60^{^o} ↺^{(4v+ 5iv + 6j^)} (1^v + 2i^{^} + 3j^v).

Here θ = 60^{^o} and v = (1^v + 2i^{^} + 3j^v).

ur is the unit of rotation for the Opposite Value (4^v+ 5i^v + 6j^{^}) which is the Opposite Value divided by its magnitude or radius. This gives a unit of rotation as follows:

(4^v+ 5i^v + 6j^v)/√(|4^v|² + |5i^v|² + |6j^{^}|²)
- = (4^v+ 5i^v + 6j^v)/√(77)
- = (4^v+ 5i^v + 6j^v)/8.77
- = (.456^v + .57i^v + .684j^v)

v_{rot =}

This leads to the following $v_{rot}$ equation:

$\begin{equation} v_{rot} = (\left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v \\ 0.684j\hat{ } \end{array} \right] \cdot \left[ \begin{array} {c} 1 ^v \\ 2 i\hat{ } \\ 3j^v \end{array} \right]) \left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v{ } \\ 0.684j\hat{ } \end{array} \right] + sin60^{\hat{ }o}(\left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v \\ 0.684j\hat{ } \end{array} \right] \times \left[ \begin{array} {c} 1 ^v \\ 2 i\hat{ } \\ 3j^v \end{array} \right]) + cos60^{\hat{ }o}((\left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v \\ 0.684j\hat{ } \end{array} \right] \times \left[ \begin{array} {c} 1 ^v \\ 2 i\hat{ } \\ 3j^v \end{array} \right]) \times \left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v \\ 0.684j\hat{ } \end{array} \right]) \end{equation</em>}$

$\begin{equation} v_{rot} = ^-2.735\left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v \\ 0.684j\hat{ } \end{array} \right] + 0.866(\left[ \begin{array} {c} 0.342 \hat{ } \\ 2.051i^v \\ 1.481j^v \end{array} \right]) + 0.5(\left[ \begin{array} {c} 0.342 \hat{ } \\ 2.015i^v \\ 1.481j^v \end{array} \right] \times \left[ \begin{array} {c} 0.456 ^v \\ 0.57 i^v \\ 0.684j\hat{ } \end{array} \right]) \end{equation</em>}$

$\begin{equation} v_{rot} = \left[ \begin{array} {c} 1.247 \hat{ } \\ 1.558 i\hat{ } \\ 1.870j\hat{ } \end{array} \right] + \left[ \begin{array} {c} 0.296 \hat{ } \\ 1.776 i^v \\ 1.288j^v \end{array} \right] + \left[ \begin{array} {c} 1.124^v \\ 0.221i \hat{ } \\ 0.57j^v\end{array} \right] \end{equation</em>}$

$\begin{equation} v_{rot} = \left[ \begin{array} {c} 0.419 \hat{ } \\ 0.003 i\hat{ } \\ 3.718j^v \end{array} \right] \end{equation</em>}$

Using the Vector Rotation functionality of the Omni Quaternion Calculator on an equivalent rotation, the point at (-1, 2, -3) rotated by 60^o around (-4, -5 ,6) moves to (0.419, 0.003, -3.718). This matches the result above.

Quaternion Equivalent

The following is a description of the Quaternion equivalent of 60^{^o} ↺^{(4v+ 5iv + 6j^)} (1^v + 2i^{^} + 3j^v).

Pure Quaternions are Quaternions without a scalar. The R3 vector in classical maths that is the equivalent of the axis (4^v+ 5i^v + 6j^{^}) is (-4, -5, 6) and of the Opposite Value to be rotated, (1^v+ 2i^{^} + 3j^v) is (-1, 2, -3).

The rotation can be represented using Quaternions as follows:

(-4, -5, 6) is (-4i – 5j + 6k) in Quaternions
The unit vector of the axis of rotation, 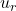, is:
- (-4i – 5j + 6k)/√(4² + 5² + 6²) = (-4i – 5j + 6k)/8.775
  - = (-0.4558i – 0.5698j + 0.6838k)
The vector to be rotated, $q_v$ at (-1, 2, -3) is (-1i + 2j – 3k) in Quaternions.
The Quaternion of Rotation, 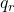, for a given unit vector (x, y, z) and angle of rotation θ is given by the formula:
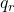- $q_r$ = cos(θ/2) + (xi + yj + zk) * sin(θ/2)
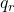- = cos(60^o/2) + (-0.4558i – 0.5698j + 0.6838k) * sin(60^o/2)
  - = 0.866 + (-0.4558i – 0.5698j + 0.6838k) * 0.5
  - = (0.866 – 0.2279i – 0.2849j + 0.3419k)
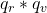rotates the Quaternion by the Quaternion of Rotation:
- (0.866 – 0.2279i – 0.2849j + 0.3419k)(-1i + 2j – 3k)
  - = (1.3676 – 0.6951i + 0.7064j – 3.3387k)

To convert a Quaternion back to an R3 vector in classical maths, the Quaternion needs to be multiplied with the conjugate of the Quaternion of Rotation which is (0.866 + 0.2279i + 0.2849j – 0.3419k).

(1.3676 – 0.6951i + 0.7064j – 3.3387k)(0.866 + 0.2279i + 0.2849j – 0.3419k)
= (0.419i + 0.003j – 3.718k)

This matches the Wave Number rotation result obtained above.

Next: Complex Rotations – Example 3

Previous: Complex Rotations – Example 1

Share to:

R3 – Complex Rotations – Example 2

Wave Number Rotation Formula

Example 2

Quaternion Equivalent

Leave a Reply Cancel reply