This post describes the role of Cartesian Coordinates and Euler’s formula in R2 Wave Number Rotation.
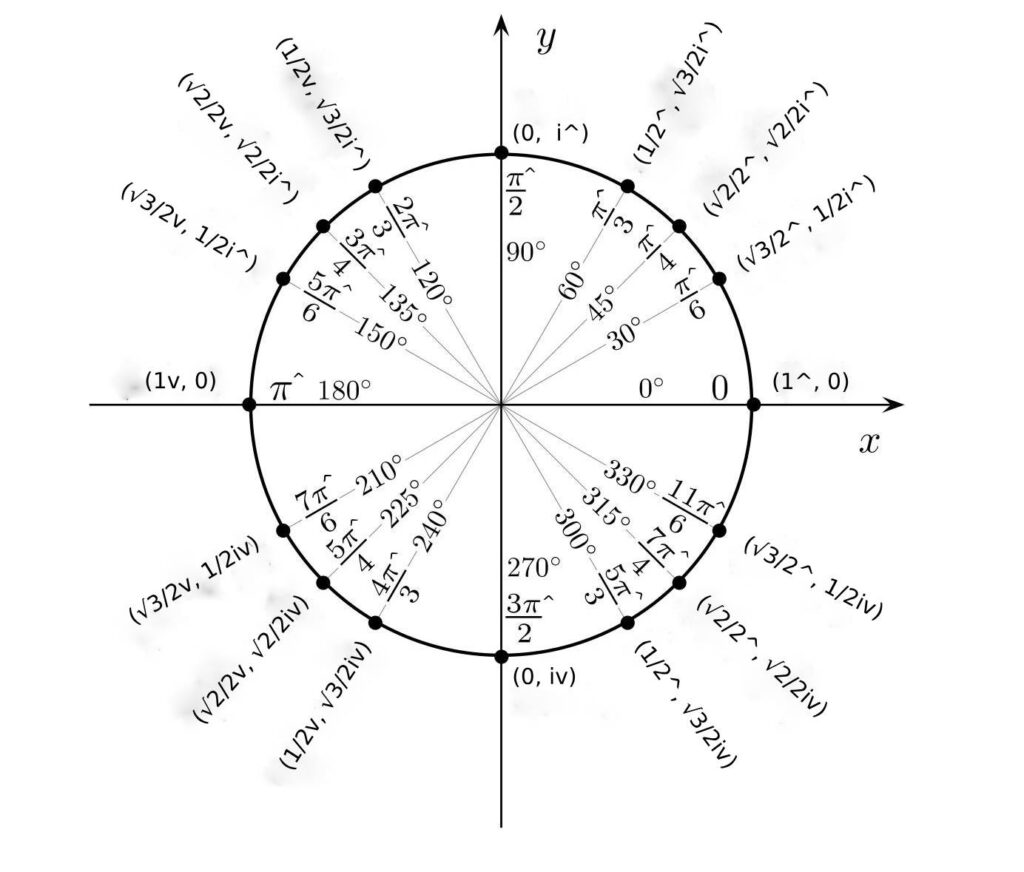
Cartesian Coordinates and Euler’s Formula in R2
The Cartesian coordinates of a point are based on the intersection of perpendicular lines from the point with the x and y axes. For example: The Cartesian coordinates at π^/4 or 45^o are (√2/2^, √2/2i^). The coordinates can be expressed algebraically as the sum of the Opposite Values (√2/2^ + √2/2i^). All Opposite Values on axes are real, so there is no need for the association of Cartesian coordinates with imaginary numbers as in classical maths.
Furthermore, calculate the coordinates of a point on the unit circle using Euler’s formula:
- ei^x = cos(x)*1^ + sin(x)*i^
ei^x takes the point (1^, 0) on the x-axis and then moves it to a point on a circle with radius of 1^. Such a movement depends on the value of x, which is in radians. Note that a ^ value is a counterclockwise rotation from the x-axis and a v is a clockwise rotation.
cos(x)*1^ represents the x-axis’ coordinate of the point. sin(x)*i^ represents the y-axis’ coordinate.
For example, the coordinates for ei^x with x = 3π^/4, 135^o can be calculated using Euler’s formula as below.
- cos (3π^/4)*1^ = –√2/2*1^ = √2/2v
- sin(3π^/4)*i^= √2/2*i^ = √2/2i^
- Giving the coordinates (0.707v, 0.707i^)
Calculating Cartesian Coordinates using Euler’s Power Series
The Power Series definition allows ei^x to be stated as:
- ei^x= 1^ +i^x + (i^x)2/2! + (i^x)3/3! + (i^x)4/4! + (i^x)5/5! …. (i^x)n/n!.
Example 1
For example, the coordinates with x = 3π^/4, 135^o can be calculated using the Power Series as in the table below.
| ei^3π^/4 | ^v Values | i^/iv Values |
| 1^ | 1^ | |
| i^3π^/4 | 2.3561i^ | |
| (i^3π^/4)2/!2 | 2.7758v | |
| (i^3π^/4)3/!3 | 2.1801iv | |
| (i^3π^/4)4/!4 | 1.2842^ | |
| (i^3π^/4)5/!5 | 0.6052i^ | |
| (i^3π^/4)6/!6 | 0.2376v | |
| (i^3π^/4)7/!7 | 0.0800iv | |
| (i^3π^/4/!8 | 0.0238^ | |
| (i^3π^/4)9/!9 | 0.0062i^ | |
| (i^3π^/4)10/!10 | 0.0015v | |
| (i^3π^/4)11/!11 | 0.0003iv | |
| : | ||
| Total | 0.707v | 0.707i^ |
Example 2
For a second example, the coordinates with x = 7πv/4, 315vo can be calculated using the Power Series as in the table below.
| ei^7πv/4 | ^v Values | i^/iv Values |
| 1^ | 1^ | |
| i^7πv/4 | 5.4978iv | |
| (i^7πv/4)2/!2 | 15.1128v | |
| (i^7πv/4)3/!3 | 27.6957i^ | |
| (i^7πv/4)4/!4 | 38.0663^ | |
| (i^7πv/4)5/!5 | 41.856i^ | |
| (i^7πv/4)6/!6 | 38.3526v | |
| (i^7πv/4)7/!7 | 30.1221iv | |
| (i^7πv/4/!8 | 20.7006^ | |
| (i^7πv/4)9/!9 | 12.6452i^ | |
| (i^7πv/4)10/!10 | 6.9521v | |
| (i^7πv/4)11/!11 | 3.4747iv | |
| (i^7πv/4)12/!12 | 1.5919^ | |
| (i^7πv/4)13/!13 | 0.6732i^ | |
| (i^7πv/4)14/!14 | 0.2644v | |
| (i^7πv/4)15/!15 | 0.0969iv | |
| (i^7πv/4)16/!16 | 0.0333^ | |
| (i^7πv/4)17/!17 | 0.2157i^ | |
| (i^7πv/4)18/!18 | 0.0033v | |
| (i^7πv/4)19/!19 | 0.0952iv | |
| : | ||
| Total | 0.707^ | 0.707i^ |
Euler’s Formula for Coordinates
In general, the (x, y) Cartesian coordinates of any point in R2 are given by Euler’s formula:
- x = rCos(ϕ)*1^ and y = rSin(ϕ)*i^
In this formula, ϕ (Phi) is the angle of rotation counterclockwise from the x-axis to the line joining origin with the point and r is the distance of a point from the origin.
Counterclockwise Rotation
Rotations with ^ radian values result in counterclockwise rotation: For example:
- ei^π^/4 at 45^o = cos(π^/4)*1^ + sin(π^/4)*i^
- = √2/2*1^ + √2/2*i^ = √2/2^ + √2/2i^
- ei^3π^/4 at 135^o = cos(3π^/4)*1^ + sin(3π^/4)*i^
- = –√2/2*1^ + √2/2*i^ = √2/2v + √2/2i^
- ei^5π^/4 at 225^o = cos(5π^/4)*1^ + sin(5π^/4)*i^
- = –√2/2*1^ + –√2/2*i^ = √2/2v + √2/2iv
- ei^7π^/4 at 315^o = cos(7π^/4)*1^ + sin(7π^/4)*i^
- = √2/2*1^ + –√2/2*iv = √2/2^ + √2/2iv
Clockwise Rotation
Rotations with v radian values result in counterclockwise rotation: For example:
- ei^πv/4 at 45vo = cos(πv/4)*1^ + sin(πv/4)*i^
- = √2/2*1^ + –√2/2*iv = √2/2^ + √2/2iv
- ei^3πv/4 at 135vo = cos(3πv/4)*1^ + sin(3πv/4)*i^
- = –√2/2*1^ + –√2/2*i^ = √2/2v + √2/2iv
- ei^5πv/4 at 225vo = cos(5πv/4)*1^ + sin(5πv/4)*i^
- = –√2/2^*1^ + √2/2*i^ = √2/2v + √2/2i^
- ei^7πv/4 at 315vo = cos(7πv/4)*1^ + sin(7πv/4)*i^
- = √2/2*1^ + √2/2*i^ = √2/2^ + √2/2i^
Next: Multiplication Table
Previous: Simple Rotations

