R2 – Roots – Definition

This post on R2 roots covers the definition of roots and how roots are derived from the R2 multiplication table. Examples of square, cube and higher roots are given.

Definition

Wikipedia defines the square root as ‘a square root of a number x is a number y such that y² = x; in other words, a number y whose square (the result of multiplying the number by itself, or ) is x.’ Wave Numbers uses this definition and adapts it for roots of higher degrees.

The ⁿ√ symbols, where n ≥ 2, represents the root of an Opposite Value. The default representation of √ without a value for n represents ²√.

There are two types of root. The first is the root of the Counter in an Opposite Value. The Counter root of an Opposite Value x is the Counter that when raised to the power of n gives the Counter of x and maintains the original Opposite Type and Opposite Sign. The fact that the Opposite Value is not within brackets identifies that it is a Counter root as in ^?√x^?.  For example: ²√1^{^} = 1^{^} and ²√i^v = ²√1i^v = i^v . In other words, ignore the rotation expressed by the Opposite Values when calculating the Counter root.

The Full Root of an Opposite Value x is the Opposite Value that when raised to the power of n gives x.  Enclose the Opposite Value by brackets in order to specify the Full root of the Opposite Value. For example: √(4^v) = 2i^{^} or 2i^v.

Calculate the full root as the square root of the Counter times the square root of the Unitary. For example: √(9^v) = √9*√(1^v)  = 3*i^{^} = 3i^{^} or = 3*i^v = 3i^v.

Designate the degree of the root in the same way as for classical maths. So, ³√8i^{^} = 2i^{^} and is the cube root of the Counter 8 and holds the same Opposite Sign.

Rotation Table

The R2 multiplication table defines the following:

• 1^{^2} = 1^{^}*1^{^} = 1^{^} => 1^{^n} = 1^{^}
• 1^v2= 1^v*1^v = 1^{^} and    1^v3 =  1^v*1^{^} = 1^v
  • => for even values of n, 1^vn = 1^{^}
  • => for odd values of n, 1^vn = 1^v
• i^{^2} = i^{^}*i^{^} = 1^v,    i^{^3} = i^{^}*1^v = i^v
• i^{^4} = i^{^}*i^v = 1^{^};   i^{^5} = i^{^}*1^{^} = i^{^}
• i^v2 =  i^v*i^v = 1^v,     i^v3 =  i^v*1^v = i^{^}     
• i^v4 = i^v*i^{^} = 1^{^};       i^v5 = i^v*1^{^} = i^v

The following can be deduced from the above:

• √(1^{^}) = 1^{^} or 1^v
• √(1^v) = i^{^} or i^v
• ⁿ√(1^{^}) = 1^{^}, 1^v for even values of n
  • = 1^{^} for odd values of n and
  • = i^{^} or i^v for values of 4n
• ⁿ√(1^v) = 1^v  for odd values of n  and
  • = i^{^}  or i^v for values of (2 +4n)

Other Roots Based on Spherical Coordinates

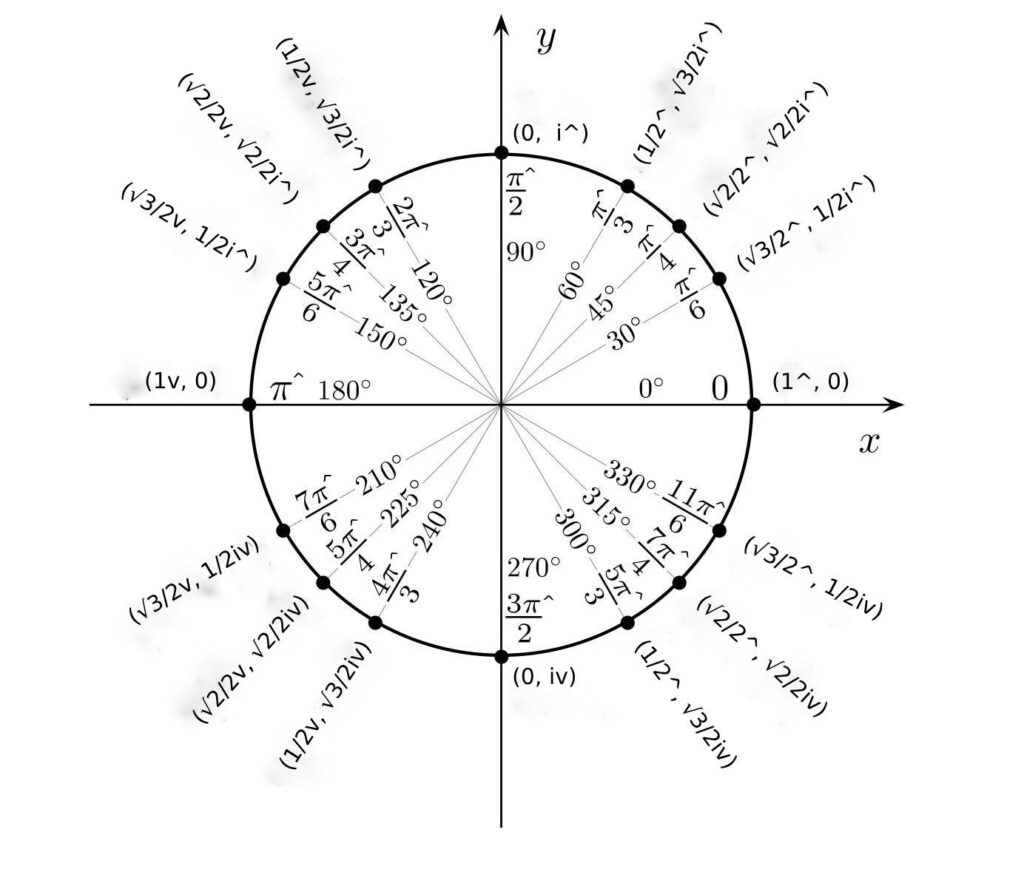
Other roots can be calculated by looking at the spherical coordinates. 1^{^} is the cube root of 1^{^}. The spherical co-ordinates of 120^{o^}, (½^v + √3/2i^{^}), are also the cube root because 3 counterclockwise rotations of 120^o from 1^{^} bring a point back to the location 1^{^}. i.e. (½^v + √3/2i^{^})* (½^v + √3/2i^{^})* (½^v + √3/2i^{^}) = 1^{^}.

The spherical co-ordinates of 240^{o^}, (½^v + √3/2i^v), are the cube root because 3 clockwise rotations of 120^o from 1^{^} bring a point back to 1^{^}. i.e. (½^v + √3/2i^v)* (½^v + √3/2i^v)* (½^v + √3/2i^v) = 1^{^}.

Number of Roots

The number of roots available are dependent on the degree. For example ³√ has 3 roots. Other examples are:

• ³√(1^{^}) = 1^{^} or (½^v + √3/2i^{^}) or (½^v + √3/2i^v)
• ⁵√(1^{^}) =  1 ^{^} or (0.309^{^} + 0.951i^{^}) or (0.309^{^} + 0.951i^v)
  • or (0.809^v + 0.588i^{^}) or (0.809^v + 0.588i^v)
• ⁴√(1^v) =  (√2/2^{^} + √2/2i^{^}) or  (√2/2^v + √2/2i^{^}) etc..
• ⁸√(1^v) = 0.924^{^} + 0.383i^{^} etc.;       

Conclusion

Try these examples of roots with our online calculator.

Next: Simple Roots

Previous: Advanced Division