Definition of the Property of Order
In Cecilia Hamm’s ‘Making Sense of Negative Numbers’ she states:
A: “For natural numbers, if ![]() and
and ![]() then
then ![]() and there exists a number
and there exists a number ![]() such that
such that ![]() and
and ![]() . Hence for any
. Hence for any ![]() N if
N if ![]() then
then ![]() . Including zero in the domain and taking
. Including zero in the domain and taking ![]() will lead to a contradiction: if
will lead to a contradiction: if ![]() then
then ![]() “
“
However, in Wave Numbers, if ![]() , then the statement
, then the statement ![]() cannot be true, as no Opposite Value is less than 0. Thus, this is not a valid example in Wave Numbers. Additionally, division by 0 is undefined in Wave Numbers.
cannot be true, as no Opposite Value is less than 0. Thus, this is not a valid example in Wave Numbers. Additionally, division by 0 is undefined in Wave Numbers.
The statement if ![]() and
and ![]() then
then ![]() needs to be qualified in Wave Numbers to exclude the cases where
needs to be qualified in Wave Numbers to exclude the cases where ![]() or
or ![]() .
.
B: “Including negative numbers in the domain and taking ![]() and
and ![]() implies that if
implies that if ![]() then
then ![]() . Taking
. Taking ![]() will lead to a contradiction: if
will lead to a contradiction: if ![]() then
then ![]() , in short: if
, in short: if ![]() then
then ![]() . This contradicts the basic property of order.”
. This contradicts the basic property of order.”
In Wave Numbers, only the magnitudes of Opposite Values can be compared using the concept of “less than.” This means only their Counters can be compared. The absolute value symbol is used to refer specifically to an Opposite Value’s Counter. For example, ![]() and
and ![]() . Therefore, the statement
. Therefore, the statement ![]() can never be true. This ensures that no contradiction of the basic property of order can occur.
can never be true. This ensures that no contradiction of the basic property of order can occur.
Example for A
Classical Math
For A above in classical math let ![]() = 3,
= 3, ![]() =2,
=2, ![]() =6 and
=6 and ![]() =4:
=4:
- 3 > 2
 >
> 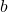 is true
is true - 3/2 = 6/4
 /
/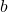 =
=  /
/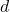 is true
is true  = ½
= ½ and
and 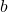 = ½
= ½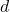
- => there exists a number
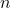 = ½ where
= ½ where  =
= 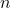 *
* and
and 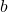 =
= 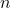 *
*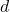
- => there exists a number
Now let ![]() = 0,
= 0, ![]() = -2,
= -2, ![]() = 0, and
= 0, and ![]() = 0 then
= 0 then ![]() /
/![]() =0/-2,
=0/-2, ![]() /
/![]() = 0/0, so
= 0/0, so ![]() /
/![]() =
= ![]() /
/![]() = 0 is true.
= 0 is true.
Here ![]() >
> ![]() =>
=> ![]() >
> ![]() but 0 > 0 is not true leading to the contradiction. Division by 0 is undefined in classical maths.
but 0 > 0 is not true leading to the contradiction. Division by 0 is undefined in classical maths.
Wave Numbers
For A above in Wave Numbers, let ![]() = 3^,
= 3^, ![]() =2^,
=2^, ![]() =6^ and
=6^ and ![]() =4^:
=4^:
- 3^ > 2^
 >
> 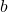 is true
is true - 3^/2^ = 6^/4^
 /
/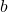 =
=  /
/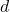 is true
is true  = ½^
= ½^ and
and 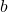 = ½^
= ½^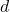
- => there exists a number
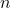 = ½^ where
= ½^ where  =
=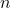 *
* and
and 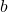 =
= 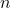 *
*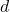
- => there exists a number
Now let ![]() = 0,
= 0, ![]() = 2v,
= 2v, ![]() = 0, and d = 0 then
= 0, and d = 0 then ![]() /
/![]() =0/2v,
=0/2v, ![]() /
/![]() = 0/0.
= 0/0.
However, if ![]() = 0, then the statement
= 0, then the statement ![]() >
> ![]() cannot be true as no Opposite Value is less than 0. So, this is not a valid example in Wave Numbers. Note also that division by 0 is undefined in Wave Numbers.
cannot be true as no Opposite Value is less than 0. So, this is not a valid example in Wave Numbers. Note also that division by 0 is undefined in Wave Numbers.
The statement ‘if ![]() >
> ![]() and
and ![]() /
/![]() =
= ![]() /d then
/d then ![]() >
> ![]() ’ needs to be qualified in Wave Numbers to exclude
’ needs to be qualified in Wave Numbers to exclude ![]() =
= ![]() = 0.
= 0.
Example for B
Classical Math
For B above in classical maths, let ![]() = 4,
= 4, ![]() = –
= –![]() = -4,
= -4, ![]() = -1
= -1
- if
 > –
> – then
then 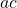 >
>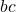
- 4 > -4, so 4*-1 > -4*-1, -4 > 4 (Not true)
- If
 > –
> – then
then 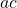 > –
> –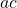 but the example shows
but the example shows 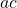 > –
> –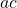 is not true ( 4*-1 < -4*-1, -4 < 4)
is not true ( 4*-1 < -4*-1, -4 < 4)
This is what contradicts the basic property of order and is one reason for the introduction of absolute values.
Wave Numbers
For B above in Wave Numbers, let ![]() = 4^,
= 4^, ![]() =
= ![]() = 4v,
= 4v, ![]() = 1v
= 1v
In Wave Numbers only the magnitudes of Opposite Values can be compared using the less than concept. i.e. only their Counters can be compared. The absolute value symbol is used to refer specifically to an Opposite Values counter. So |4^| = |4v| and |![]() | = |-
| = |-![]() |. This means that the statement if |
|. This means that the statement if |![]() | > |-
| > |-![]() | can never be true. So, no contradiction of the basic property of order can occur.
| can never be true. So, no contradiction of the basic property of order can occur.
Next: R1
Previous: Ratios

