This post covers the features of single and multipart qubits.
Single Qubit Features
- A qubit is described by the equation (a|jˆ> + b|jv>) and is derived from the generic formula for a quantum state: |ψ> = cos (𝜭/2) |jˆ> + eiϕ sin( 𝜭/2) |jv>.
- The σx gate inverts a qubit. For example: it allows |j^> to change to |jv>, –|j^> to change to –|jv> and vice versa.
- The top row and bottom row of a qubit’s matrix can be multiples of either 0, ^, v, i^ or iv Opposite Values.
- A qubit of the equivalent of 5|j^> + 3|jv> qubits is normalised in the equation:
- 5/√(52 + 32)|j^> + 3/√(52 + 32)|jv>
- = 5/√(34)|j^> + 3/√34)|jv>
Flip Operation
- The flip operation is the short for the σf gate, denoted by –, and changes the signs of both elements of the qubit. For example:
- –|j^> = –
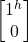 =
=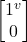
- –|j^> = –
- – –|j^> = – –
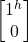 =–
=–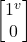 =
=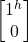
- –|^> = –
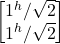 =
=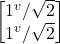
- –|v> = –
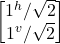 =
=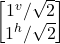
- –|i^> = –
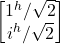 =
=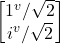
- –|iv> = –
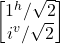 =
=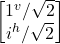
- Flipped qubits cancel each other out. For example: |jv> + –|jv> = 0
Multipart Qubit Features
- Quantum computers use single qubits to form multipart qubits in multipart qubit circuits
- Quantum computers execute programs using multipart qubit circuits.
- Represent the multipart qubit |jvj^j^> in a matrix as follows:
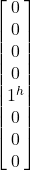
- Note that the next post on matrices shows how the tensor product is used to set up multipart qubits
- |jvj^j^> ≠ |j^jvj^> ≠ |j^j^jv>
- However, |–jvj^j^> = |jv-j^j^> = |jvj^-j^> = –|jvj^j^>
- A column of bits forms a multipart qubit. An odd number of flips, –, results in a flip sign preceding a multipart qubit. For example:
- |–jvj^j^> = |jv-j^j^> = |jvj^-j^> = –|jvj^j^>
- =

- Note that the post on next post on matrices shows the calculation of this multipart qubit.
- A column of bits forms a multipart qubit. An odd number of flips, –, results in a flip sign preceding a multipart qubit. For example:
- In the multipart qubits |00100> + –|01100> the second part is flipped. Determine the flip sign of a part of a multipart qubit by the elements of the qubit. An odd number of v Opposite Signs require a flip to proceed the part.
- Primary and dependent single qubits make up a multipart qubit
Superposition and Entanglement and Mega Qubits
- A qubit splitter changes |j^> or |jv> into superposition and forms a mega qubit. For example: A Hadamard gate splits |j^> into the mega qubit |j^> + |jv> and splits |jv> into the mega qubit |j^> + –|jv>.
- Only the primary qubits of a multipart qubit are put in superposition because the others will get there after the implementation of dependencies.
- The number of possible independent states is 2n where n is the number of primary qubits. These possible independent states form a mega qubit.
- Entangled qubits are orthogonal within each qubit and between states. For example: In the entangled multipart qubit: |ψ> = 1^/√2(|j^j^> + –|jvjv>):
- The first qubit Q0 state is |j^> + –|jv> as follows:
- Q0 =
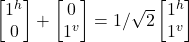
- The two elements within Q0 are orthogonal
- Q0 =
- The second qubit Q1 represents |j^> + –|jv> as follows:
- Q1 =
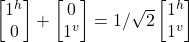
- The two elements within Q1 are orthogonal
- Q1 =
- The states |j^j^> and –|jvjv> are orthogonal because
- <j^j^|.–|jvjv> = [1^ 0 0 0]
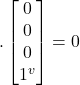
- <j^j^|.–|jvjv> = [1^ 0 0 0]
- The first qubit Q0 state is |j^> + –|jv> as follows:
Next: Matrices
Previous: Basis and Born’s Rule

