This post describes the new Wave Numbers Bloch sphere. The sphere has been redesigned to use R2 Wave Numbers. Our shop does not have the Wave Numbers Bloch sphere available yet. However, the classic Bloch Sphere rotation ball is available.
Quantum Bases
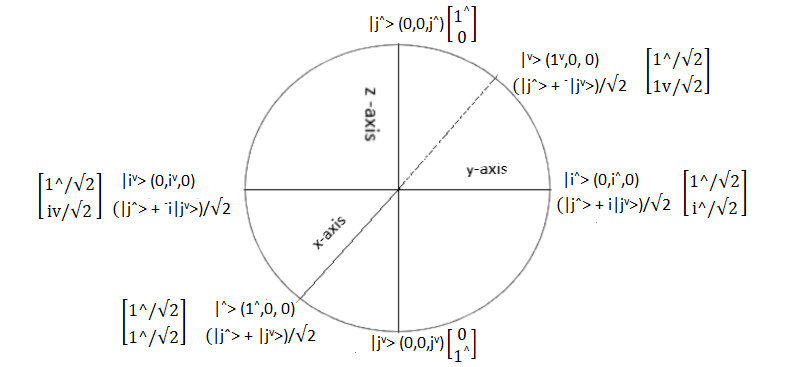
Basis defined by |j^> and |jv> states
The states that make up a basis for any classical qubit are |0> and |1>. It is possible to write any qubit state as a combination of these two states.
The state |0> on the Wave Numbers Bloch sphere is now |j^> as it is on the z-axis at the north pole. Its R3 coordinates are (0, 0, j^) and its matrix representation is ![]() .
.
Please note that a solution to displaying ^, i^ or j^ in a matrix using Latex has not been found, so for the moment the ^ superscript is replaced with the h for Hat superscript.
Naming the state |j^> instead of |0> breaks the link with the number 0. To call a state 0 is to imply that it is a nothing state, an absence of state. In reality |0> represents that the qubit is located in the northern hemisphere.
The state |1> is now |jv> as it is on the z-axis at the south pole. Its R3 coordinates are (0, 0 , jv) and its matrix representation is ![]() .
.
Basis defined by |^> and |v> states
The states |+> and |-> form the Haadamard basis.
The state |+> is now |^> as it is on the x-axis at the near pole. Its R3 coordinates are (1^, 0, 0) and its matrix representation is ![]() . So, |^> = (|j^> + |jv>)/√2 and this combination of states is the equivalent of the Cartesian coordinate (1^, 0, 0).
. So, |^> = (|j^> + |jv>)/√2 and this combination of states is the equivalent of the Cartesian coordinate (1^, 0, 0).
The state |-> is now |v> as it is on the x-axis at the far pole. Its R3 coordinates are (1v, 0, 0) and its matrix representation is ![]() . So, |v> = (|j^> + –|jv>)/√2 .
. So, |v> = (|j^> + –|jv>)/√2 .
Basis defined by States |i^> and |iv>
The states |+> and |-> form the Haadamard basis states.
The state |i> is now |i^> as it is on the y-axis at the east pole. Its R3 coordinates are (0, i^,0) and its matrix representation is ![]() . So, |i^> = (|j^> + i|jv>)/√2 .
. So, |i^> = (|j^> + i|jv>)/√2 .
The state |-i> is now |iv> as it is on the y-axis at the west pole. Its R3 coordinates are (0,iv,0) and its matrix representation is ![]() . So, |iv> = (|j^> + –i|jv>)/√2 .
. So, |iv> = (|j^> + –i|jv>)/√2 .
Wave Numbers Bloch Sphere vs Cartesian Space
Angles on the Bloch sphere are twice as big as in Hilbert Space. Wikipedia defines a Hilbert Space as ‘a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space.’
This means that any 2 vectors that are orthogonal (90o) in Hilbert or Cartesian space are parallel and in opposite directions on the Bloch Sphere such as the vectors on the x-axis represented by |j^> and |jv>. The dot product of their matrices ![]() = 0, which shows that the two states are orthogonal. This is the reason that 𝜭 to divide by 2 in the generic formula for a quantum state that is described in the next post.
= 0, which shows that the two states are orthogonal. This is the reason that 𝜭 to divide by 2 in the generic formula for a quantum state that is described in the next post.
The states |j^> and |jv> are orthogonal because of the dot-product rule and represent the Cartesian coordinates (0, 0 , j^) and (0, 0, jv). However the Cartesian coordinates (0, 0 , j^) and (0, 0, jv) are not orthogonal as they are 180o apart. There are links between the Bloch Sphere and 3D Cartesian Sphere but they are not the same.
Qubit Measurements
The goal of qubit measurement is to determine whether the qubit has a value of j^ or jv. In physical terms this means that the electron is either in the northern hemisphere or the southern hemisphere. Any position in the northern hemisphere will return a result of j^ and any in the southern of jv. This means that pure states with values of ![]() measure as j^. Pure states with values of
measure as j^. Pure states with values of ![]() will be measured as jv.
will be measured as jv.
States such as ![]() have a 50% chance of measuring as j^ and 50% as jv.
have a 50% chance of measuring as j^ and 50% as jv.
Next: State Equations
Previous: Classical Qubits

