Why Simultaneous Equations are Needed
According to the theorem of multiplicative inverses, R3 lacks multiplicative inverses. Therefore, the Wave Number system employs an alternative method to compute the result of division in R3, using simultaneous equations.
Consider the following equation:
To obtain the result of the division, you need to solve the following equation:
The following method involves using simultaneous equations to determine the result of dividing R3.
Method
Step 1: Identifying the R3 Simultaneous Equations Needed for Division
Rewrite the equation above as:
The expression ![]() serves as the Operator of the multiplication and is represented by
serves as the Operator of the multiplication and is represented by ![]() . Each element corresponds to an axis of one of the three rotations of the multiplication. The Operand of the division is
. Each element corresponds to an axis of one of the three rotations of the multiplication. The Operand of the division is ![]() and is represented by
and is represented by ![]() .
.
The formulae for calculating multiplication are:
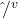 value:
value: 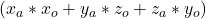
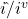 value:
value: 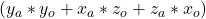
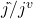 value:
value: 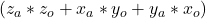
Accordingly, this gives three equations:
- A:
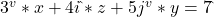
- B:
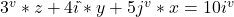
- C:

Step 2: Transforming into Simultaneous Equations
Equation A
Transform Equation A into a simultaneous equation as follows:
The multiplication table indicates that the product of Opposite Values of a ![]() with a
with a ![]() results in a
results in a ![]() value that retains the sign of the operand. Thus,
value that retains the sign of the operand. Thus, ![]() becomes
becomes ![]()
Similarly ![]() produces a
produces a ![]() value with the same sign as in
value with the same sign as in ![]() . Thus,
. Thus, ![]() becomes
becomes ![]() .
.
Likewise, ![]() results in a
results in a ![]() value with the same sign as in
value with the same sign as in ![]() . Thus,
. Thus, ![]() becomes
becomes ![]() .
.
The Opposite Sign of the result is ![]() and so the result becomes
and so the result becomes ![]() .
.
The Opposite Types and Signs have been eliminated, yielding equation A-modified:
Equation B
Transform Equation B into a simultaneous equation as follows:
The product of a ![]() and a
and a ![]() or
or ![]() result in an
result in an ![]() that retains the sign of the operand. So,
that retains the sign of the operand. So, ![]() becomes
becomes ![]() .
.
Similarly ![]() becomes
becomes ![]() with the same sign as in
with the same sign as in ![]() .
.
However, the product of a ![]() and an
and an ![]() results in a sign reversal, thus
results in a sign reversal, thus ![]() becomes
becomes ![]() .
.
The Opposite Sign of the result is ![]() and so the result becomes
and so the result becomes ![]() .
.
Equation C
Finally, equation C generates the following simultaneous equation C-modified:
Step3: Solving the R3 Simultaneous Equations for Division
Substituting for ![]() from Equation C-modified into Equation A-modified above gives:
from Equation C-modified into Equation A-modified above gives:
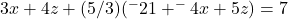
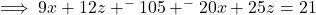
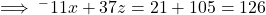 giving Equation D
giving Equation D
Secondly, a similar substitution for ![]() in Equation B-modified above gives:
in Equation B-modified above gives:
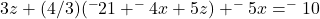
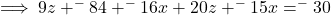
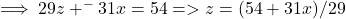 giving Equation E
giving Equation E
Thirdly, substituting for ![]() from Equation E into Equation D gives:
from Equation E into Equation D gives:
Next, substituting for ![]() with
with ![]() in Equation D gives:
in Equation D gives:
Finally, substituting for ![]() with
with ![]() and
and ![]() with
with ![]() in Equation A-modifed gives:
in Equation A-modifed gives:
The variable ![]() represents the
represents the ![]() Counter and is
Counter and is ![]() and so gives a solution for
and so gives a solution for ![]() of
of ![]() . The variable
. The variable ![]() represents the
represents the ![]() Counter and is
Counter and is ![]() and so gives a solution for
and so gives a solution for ![]() of
of ![]() . The variable
. The variable ![]() represents the
represents the ![]() Counter and is
Counter and is ![]() and so gives a solution for
and so gives a solution for ![]() of
of ![]() . So, the overall solution is
. So, the overall solution is ![]() .
.
Next: Roots
Previous: Multiplicative Inverses

