Up to this point, we’ve focused on unitary rotations around a single axis on the unit sphere. Now, let’s delve into more complex rotations in R3, where the operand can be any combination of Opposite Values with any degree of rotation. This post introduces the Wave Number Rotation formula, based on Rodrigues’ formula for calculating rotation along with the first of 3 examples of complex rotation:
Rodrigues’ Formula
In terms of Tait-Bryan Intrinsic rotation, more complex rotations are made up of z-y’-x’’ rotation using the Tait-Bryan angles with any values of φ, θ and ψ. However, using a 3-step process to calculate rotation can lead to Gimbal lock. This causes the loss of correct orientation.
A single axis-angle rotation around any vector through the origin overcomes Gimbal lock. Rodrigues’ rotation formula supports a single axis-angle rotation:
![]()
In this formula:
 is the vector being rotated.
is the vector being rotated.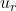 is the unit vector representing the axis of rotation.
is the unit vector representing the axis of rotation.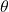 is the angle of rotation.
is the angle of rotation.
The “.” in the formula represents the dot product of two Opposite Values. The post on dot product explains this calculation. The “x”s in the in the formula represents the cross product of two Opposite Values. The post on cross product explains these calculations.
This approach allows for the calculation of rotations around any vector through the origin, effectively handling complex rotations in ![]() .
.
Rewrite the vrot formula as:
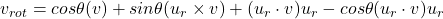
- Rewrite
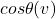 as
as 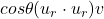 because
because 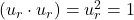 since
since  is the unit vector.
is the unit vector. 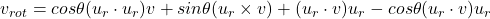
- The vector triple product rule states that
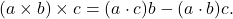
- So,
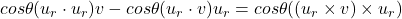
- giving
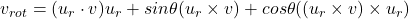
- So,
Wave Numbers uses this formula to calculate rotation in R3.
Checking the Results of Rotation in R3
All the examples of rotation are checked using the online calculator available on the top menu. They are also cross-checked against the equivalent vector rotations using the Quaternion Calculator which is one of the many calculators in the Omni Calculator. The equivalent quaternion calculation follows each example.
Example 1
Take for example 60^o ↺(4^+ 5i^ + 6j^) (1^ + 2i^ + 3j^).
- Here θ = 60^o and v = (1^ + 2i^ + 3j^).
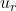 is the unit of rotation for the Opposite Value (4^+ 5i^ + 6j^) that is the Opposite Value divided by its magnitude or radius. This gives a unit of rotation as follows:
is the unit of rotation for the Opposite Value (4^+ 5i^ + 6j^) that is the Opposite Value divided by its magnitude or radius. This gives a unit of rotation as follows:- (4^+ 5i^ + 6j^)/√(|4^|2 + |5i^ |2 + |6j^|2)
- = (4^+ 5i^ + 6j^)/√(77)
- = (4^+ 5i^ + 6j^)/8.77
- = (.456^ + .57i^ + .684j^)
This leads to the following ![]() equation:
equation:
![Rendered by QuickLaTeX.com \begin{equation} v_{rot} = (\left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right] \cdot \left[ \begin{array} {c} 1 \hat{ } \\ 2 i\hat{ } \\ 3j\hat{ } \end{array} \right]) \left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right] + sin60^{\hat{ }o}(\left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right] \times \left[ \begin{array} {c} 1 \hat{ } \\ 2 i\hat{ } \\ 3j\hat{ } \end{array} \right]) + cos60^{\hat{ }o}((\left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right] \times \left[ \begin{array} {c} 1 \hat{ } \\ 2 i\hat{ } \\ 3j\hat{ } \end{array} \right]) \times \left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right]) \end{equation</em>}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-91f755e79c37611d9ab19bcd8d73aef5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation} v_{rot} = 3.648\left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right] + 0.866(\left[ \begin{array} {c} 0.342 \hat{ } \\ 0.684 i^v \\ 0.342j\hat{ } \end{array} \right]) + 0.5(\left[ \begin{array} {c} 0.342 \hat{ } \\ 0.684 i^v \\ 0.342j\hat{ } \end{array} \right] \times \left[ \begin{array} {c} 0.456 \hat{ } \\ 0.571 i\hat{ } \\ 0.684j\hat{ } \end{array} \right]) \end{equation</em>}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-63d4cbd3d9b0110ef9df75daf34abf25_l3.png)
![Rendered by QuickLaTeX.com \begin{equation} v_{rot} = \left[ \begin{array} {c} 1.662 \hat{ } \\ 2.078 i\hat{ } \\ 2.494j\hat{ } \end{array} \right] + \left[ \begin{array} {c} 0.296 \hat{ } \\ 0.592 i^v \\ 0.296j\hat{ } \end{array} \right] + \left[ \begin{array} {c} 0.331^v \\ 0.39i^v \\ 0.253j\hat{ } \end{array} \right] \end{equation</em>}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-f7d4f10d18e5f387c6deb4320450dea2_l3.png)
![Rendered by QuickLaTeX.com \begin{equation} v_{rot} = \left[ \begin{array} {c} 1.627 \hat{ } \\ 1.447 i\hat{ } \\ 3.043j\hat{ } \end{array} \right] \end{equation</em>}](https://wavenumbers.com/wp-content/ql-cache/quicklatex.com-289f84684103667238bdce266f46b9a2_l3.png)
Note that the magnitude of the axis of rotation is not relevant as rotation does not involve magnitude.
Equivalent R3 Rotation
Using the Vector Rotation functionality of the Omni Quaternion Calculator for an equivalent rotation in ![]() , the point at (1, 2, 3) rotated by 60^o around (4, 5, 6) moves to (1.627, 1.447, 3.043). This matches the Wave Number rotation result obtained above.
, the point at (1, 2, 3) rotated by 60^o around (4, 5, 6) moves to (1.627, 1.447, 3.043). This matches the Wave Number rotation result obtained above.
The radius of the starting point is:
The radius of the end point is:
The radii are the same as is expected after rotation.
Quaternion Equivalent
The following is a description of the quaternion equivalent of 60^o ↺(4^+ 5i^ + 6j (1^ + 2i^ + 3j^).
Pure quaternions are quaternions without a scalar. The ![]() vector equivalent in classical mathematics for the axis (4^ + 5i^ + 6j^) is (4, 5, 6) and for the Opposite Value rotated (1^+ 2i^ + 3j^) is (1, 2, 3).
vector equivalent in classical mathematics for the axis (4^ + 5i^ + 6j^) is (4, 5, 6) and for the Opposite Value rotated (1^+ 2i^ + 3j^) is (1, 2, 3).
Quaternions represent the rotation as follows:
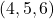 is
is 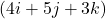
The unit vector of the axis of rotation:
-
 is
is 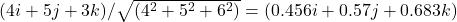
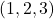 is
is 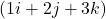
The following formula gives the quaternion of rotation, ![]() , for a given unit vector
, for a given unit vector ![]() and angle of rotation
and angle of rotation ![]()
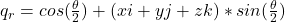
- So,
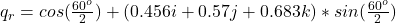
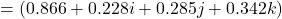
![]() rotates the vector by the quaternion of rotation:
rotates the vector by the quaternion of rotation:
![]()
To convert a quaternion back to an ![]() vector in classical maths, multiply the quaternion with the conjugate of the quaternion of rotation which is
vector in classical maths, multiply the quaternion with the conjugate of the quaternion of rotation which is ![]()
This matches the Wave Number rotation result obtained above.
Next: Complex Rotations – Example 2
Previous: Reversal, Remain and Zero Rules

