This post gives some simple R2 examples of clockwise and counterclockwise rotations around the origin.
Counterclockwise Examples
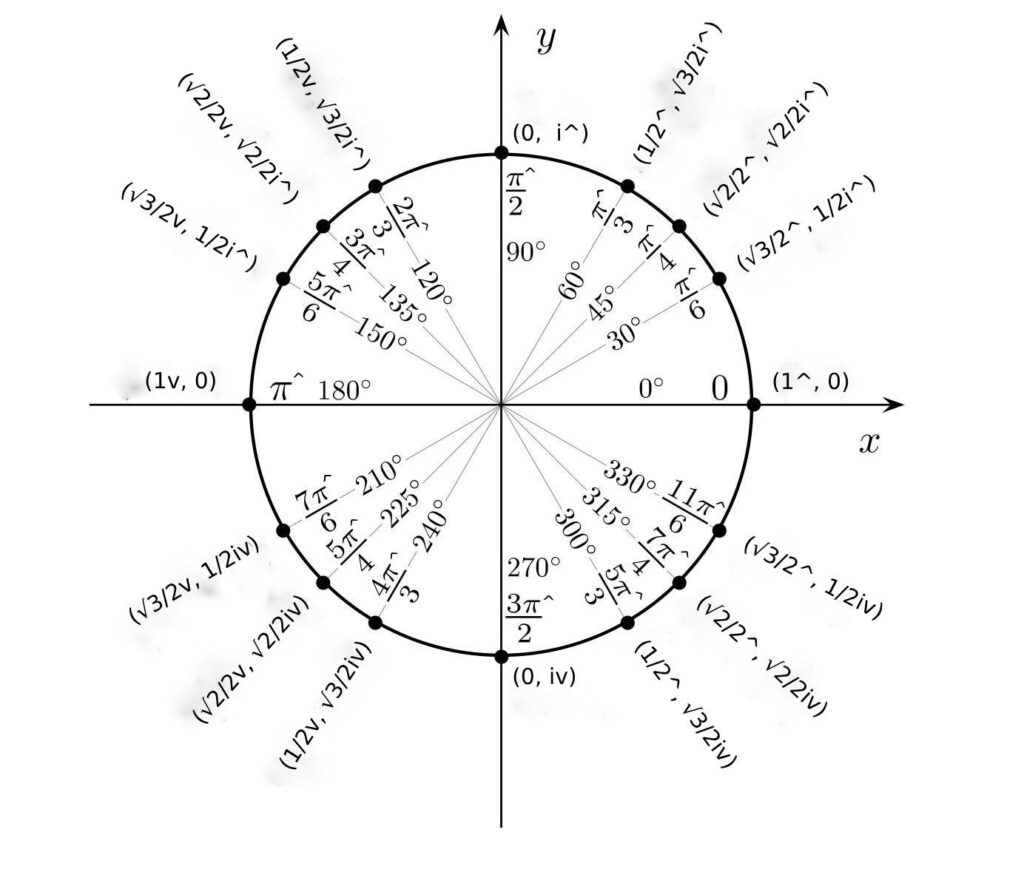
- π^/6 ↺ 1^ = √3/2^ + 1/2i^: The point (1^, 0) on the x-axis rotates by π^/6, 30o^ to the Cartesian point (√3/2^, 1/2i^). That is to say (√3/2^ +1/2i^) algebraically.
- π^/4 ↺ 1^ = √2/2^ + √2/2i^: The point (1^, 0) on the x-axis rotates by π^/4, 45o^ to the Cartesian point (√2/2^, √2/2i^). That is to say (√2/2^ + √2/2i^) algebraically.
- π^/3 ↺ 1^ = 1/2^ + √3/2i^: The point (1^, 0) on the x-axis rotates by π^/3, 60o^ to the Cartesian point (1/2^, √3/2i^). That is to say (1/2^ + √3/2i^) algebraically.
- π^/2 ↺ 1^ = i^: The point (1^, 0) on the x-axis rotates by 90o^ or π^/2 to move to the Cartesian point (0, i^). That is to say i^ algebraically.
- 2π^/3 ↺ 1^ = 1/2v + √3/2i^: The point (1^, 0) on the x-axis rotates by 2π^/3, 120o^ to the Cartesian point (1/2v, √3/2i^). That is to say (1/2v + √3/2i^) algebraically.
- 3π^/4 ↺ 1^ = √2/2v + √2/2i^: The point (1^, 0) on the x-axis rotates by 3π^/4, 135o^ to the Cartesian point (√2/2v, √2/2i^). That is to say √2/2v + √2/2i^ algebraically.
- 5π^/6 ↺ 1^ = √3/2v + 1/2i^: The point (1^, 0) on the x-axis rotates by π^/6, 150o^ to the Cartesian point (√3/2v, 1/2i^). That is to say (√3/2v +1/2i^) algebraically.
- π^ ↺ 1^ = 1v: The point (1^, 0) on the x-axis rotates by 180o^ or π^ to move to the Cartesian point (1v, 0). That is to say 1v algebraically.
- 7π^/6 ↺ 1^ = √3/2v + 1/2iv: The point (1^, 0) on the x-axis rotates by 7π^/6, 210o^ to the Cartesian point (√3/2v, 1/2iv). That is to say (√3/2v + 1/2iv) algebraically.
- 5π^/4 ↺ 1^ = √2/2v + √2/2iv: The point (1^, 0) on the x-axis rotates by 5π^/4, 225o^ to the Cartesian point (√2/2v, √2/2iv). That is to say √2/2v + √2/2iv algebraically.
- 4π^/3 ↺ 1^ = 1/2v + √3/2iv: The point (1^, 0) on the x-axis rotates by 4π^/3, 240o^ to the Cartesian point (1/2v, √3/2iv). That is to say (1/2v + √3/2iv) algebraically.
- 3π^/2 ↺ 1^ = iv: The point (1^, 0) on the x-axis rotates by 270o^ or 3π^/2 to move to the Cartesian point (0, iv). That is to say iv algebraically.
- 5π^/3 ↺ 1^ = 1/2^ + √3/2iv: The point (1^, 0) on the x-axis rotates by 5π^/3, 300o^ to the Cartesian point (1/2^, √3/2iv). That is to say (1/2^ + √3/2iv) algebraically.
- 7π^/4 ↺ 1^ = √2/2^ + √2/2iv: The point (1^, 0) on the x-axis rotates by 7π^/4, 315o^ to the Cartesian point (√2/2^, √2/2iv) that is to say (√2/2^ + √2/2iv) algebraically.
- 11π^/6 ↺ 1^ = √3/2^ + 1/2iv: The point (1^, 0) on the x-axis rotates by 11π^/6, 330o^ to the Cartesian point (√3/2^, 1/2iv). That is to say (√3/2^ +1/2iv) algebraically.
- 2π^ ↺ 1^ = 1^: The point (1^, 0) on the x-axis rotates by 360o^ or 2π^ to move back to the Cartesian point (1^, 0). That is to say 1^ algebraically.
- π^/2 ↺ 1^ = i^: The point (1^, 0) on the x-axis rotates by π^/2 to move to the Cartesian point (0, i^). That is to say i^ algebraically.
- π^/2 ↺ i^ = 1v: The point (0, i^) on the y-axis rotates by π^/2 to move to the Cartesian point (1v, 0). That is to say 1v algebraically.
- π^/2 ↺ 1v = iv: The point (1v, 0) on the x-axis rotates by π^/2 to move to the Cartesian point (0, iv). That is to say iv algebraically.
- π^/2 ↺ iv = 1^: The point (0, iv) on the y-axis rotates by π^/2 to move to the Cartesian point (1^, 0). That is to say 1^ algebraically. These last 4 rotations return the point to the beginning 1^.
Other R2 Rotations
A similar set of clockwise R2 rotations can be done using v values of π. For example: πv/2 ↺ 1^ = iv:
Other R2 rotation values of π^ or πv allow the movement of a point to anywhere on a circle. This circle will have a radius of the distance from the point to the axis point.
Conclusion
Try these examples of R2 rotation with our online calculator.
Next: Cartesian Coordinates and Euler
Previous: Rotation, Flipping and Prop

